COMP 200 & COMP 130

Edit Distance Algorithms

If you have two sets of data, how far "apart" are they? How can we measure the "similarity" between two sets of data? Such information is useful in a wide variety of fields from comparing texts to confirm authorship to comparing DNA sequences in genetic and forensic analysis. In this discussion, we will explore the path of discovery by tracing the thought processes that a practicing scientist would use to tackle this problem.

We will use the example here of comparing two strings, which are simply ordered collections of characters, but the techniques described here are generalizable to sets of any kind of data.

There are many different ways to define the "distance" between two strings. One class of measurements the minimum number of edit operations it takes to transform one string to the other, the "edit distance". Here's the classic and simplest one:

Definition of the "Levenshtein Edit Distance":

The edit distance between two strings is the number of single character manipulations (insertion, deletion or replacement) that are needed to transform one string into the other.

The edit distance thus describes how similar or dissimilar two strings are by the number of steps it takes to turn from one into the other, where a step is defined as a single character change. Not an unreasonable definition, though it is important to remember that such definitions are neither unique nor immune to changing viewpoints on the world and its relationships. In general, one shoots for definitions of relationships that exemplify the key notions in any particular world view.

Edit distance example

What is the edit distance between "SEA" and "ATE"?

At any given point we are looking at the last letter of a substring of "SEA", the source, and comparing it agains the last letter of a substring of "ATE", the target. We can characterize the difference as either an insertion of a character onto the target, a deletion of a character on the source or a replacement of the character on the source with the character on the target. We then look at new substrings that differ from the old ones by the designated edit operation. We keep track of the total number of edits until we have finally achieved the net result of transforming "SEA" into "ATE".

Here's one path to transform "SEA" into "ATE".

Step	Comparison	Edit necessary	Total Editing
1.	"S" to ""	delete: +1 edit	"S" to "" in 1 edit
2.	"E" to ""	delete: +1 edit	"SE" to "" in 2 edits
3.	"A" to "A"	no edits necessary!	"SEA" to "A" in 2 edits
4.	"A" to "T"	insert: +1 edit	"SEA" to "AT" in 3 edits
5.	"A" to "E"	insert: +1 edit	"SEA" to "ATE" in 4 edits

The edit path is not unique, as here is another path, with a shorter edit distance:

Step	Comparison	Edit necessary	Total Editing
1.	"" to ""	no edit necessary!	"" to "" in 0 edits
2.	"S" to "A"	replace: +1 edit	"S" to "A" in 1 edit
3.	"S" to "T"	insert: +1 edit	"S" to "AT" in 2 edits
4.	"E" to "E"	no edits necessary!	"SE" to "ATE" in 2 edits
5.	"A" to "E"	delete: +1 edit	"SEA" to "ATE" in 3 edits

Is this the shortest edit distance that can be found between "SEA" and "ATE"? Does it matter if more than one path have the same edit distance? Can we come up with an algorithm to find the shortest edit distance between two strings? To attack the problem of calculating the edit distance between two strings we will employ one of the most important and common algorithmic techniques in use:

Dynamic Programming

So how does one go about attacking a large problem? Well, it's just like "How do you eat an elephant?...One bite at a time!" That is, we need to break the problem down into smaller pieces that we can solve. The final solution thus becomes the result of putting all the sub-solutions together.

Dynamic programming is a general technique of reducing a large complex problem into smaller, more manageable sub-pieces that are easier to solve. Dynamic programming is characterized by

Breaking the problem down into smaller pieces.
Repeatedly ("recursively") performing the same decomposition on successively smaller and smaller pieces until a solvable piece is encountered.
Defining a solution in terms of the solutions to the smaller pieces, which may involve defining sub-solutions in terms of their relatively smaller sub-problems.

Dynamic programming is a more general application of the classic divide-and-conquer techniques, where the sub-problems are not necessarily disjoint. The fact that the sub-problems could overlap can cause calculational issues, as is discussed below.

Recurrence Relations

In order to break something down from large pieces to small pieces, we have to figure out how the large pieces of the problem relate to their smaller constituent sub-problems. Often, this is a simple, succinct articulation of a fundamental relationship(s) in the system. Avoid the temptation to become overly complicated and detailed at this stage. Novices tend to mix in excessive implementation details instead of focussing on the fundamental relationships in the problem.

Consider the edit process of transforming one string to another as a path through a set of sub-string pairs, where each pair represents the results of all the edit operations up to that point. One element of the pair is the partially deconstructed source string and the other element is the partially constructed target string.

Now consider the path, not necessairly unique, that embodies the least number of edits to fully transform the source string into the target string. Given that condition, it is asserted that the following must be true:

The path represented by any sub-string pairs on the minimum edit path, themselves are minimum edit paths from the start to the point represented by that pair.

This statement is very much akin to the logic used by the famous computer scientist and mathematician, Edsger Dijkstra, in his classic shortest path algorithm to find the shortest distance between any two points in mesh of interconnected points.

Turning the above statement around, we can say the following:

The shortest edit path to any given resultant strings must pass through the sub-string pair with the shortest edit path that immediately precedes the current state.

Since one step along the edit path is a single edit process, or a no-op if the next letter are already in place,we see that the current edit path length is zero or only one more than shortest path that leads up to it.

A statements such as the above constitute recurrence relations that relate the current state as a result of its predecessor states. With this simple recurrence relationship in hand, we can bring in the power of mathematical induction to formalize the process and step us closer to a Python realization of the algorithm.

Inductive Representation of the Recurrence Relations

Now that we have a hold on the fundamental recurrence relations in the problem, we can bring some formalism to bear on the problem. The process of breaking a problem down into successive steps is formalized in mathematics as induction. We can use this formalism to bring some structure and concreteness to our emerging algorithm.

Key to solving a problem using dynamic programming is to clearly state the recurrence relations which state how the sub-pieces relate to the whole. This amounts to the statement of the base and inductive cases that are fundamental to inductive proofs:

Base cases:

The edit distance between any string, S, (i.e. either string A or B) and an empty string is len(S), i.e. just insert all the characters in S or delete all the characters in S, depending on which way you look at it.

Inductive cases:

We can analyze two substrings, one of length i, one of length j, in terms of smaller substrings, breaking the analysis into 4 distinct situations:

Both smaller substrings are one element smaller, i.e. lengths i-1 & j-1 respectively: A[:i-1], B[:j-1]
- This corresponds to doing nothing if the current character is the same for both A and B, or
- This corresponds to replacing the last letter in A with the last letter in B if the current characters are different.
Only one substring is smaller, i.e
- A[:i-1], B[:j] -- This corresponds to performing an insertion on the "B" substring to make it the same as the "A" string.
- A[:i], B[:j-1] - This corresponds to performing an deletion on the "B" substring ("j" indices) to make it the same as the "A" string ("i" indices).

It is important to note that the details about "replacements" (substitutions), "insertions" and "deletions" etc are almost immaterial to what is going on here, for several reasons:

Other edit distance definitions include more types of operations
For more general problems, such as DNA sequence analysis, the edit operations are different.
The edit distance algorithm doesn't actually care about what the operation performed is, just that it was performed, thus raising the edit count by one.

A First Shot

In general, the approach to try first is the one that most closely matches your articulation of the problem.

Here, this means writing code that directly expresses the above stated notion that the edit distance is either the length of one string if the other string is empty (base cases) or the minimum edit distance of the 3 possible sub-string problems, plus either 0 or 1, depending on if an additional edit is necessary (inductive cases). Technically, this process is called "recursion".

Here's a very compact implementation of the above recurrence relationships

(Python syntax reminders: Strings are effectively lists of characters. aList[-1] is the last element of a list. aList[:-1] is a sub-list with every element except the last one.)

def lev(a, b):
    """Recursively calculate the Levenshtein edit distance between two strings, a and b.
    Returns the edit distance.
    """ 
    if("" == a): 
        return len(b)   # returns if a is an empty string
    if("" == b): 
        return len(a)   # returns if b is an empty string
    return min(lev(a[:-1], b[:-1])+(a[-1] != b[-1]), lev(a[:-1], b)+1, lev(a, b[:-1])+1)  # Note: True=1 and False=0 when adding a boolean to an integer

Reference: Wikibooks -- Notes: The direction through strings that the published "lev()" algorithm runs is backwards from the above code. Also, the other edit distance funcitons shown in this reference is NOT the same as discussed below!

Question: The problem with the above code is that it runs very ineffeciently. Can you find the unnecessary calculations that it performs?

Top-down vs. Bottom-up Dynamic Programming

Two possible general techniques on how to deal sub-problems:

Top-down: Try to solve the current problem ("super-problem"), which requires solving specific sub-problems.
- Pros: Easy to conceptualize as it tends to matches the recurrence relationship, which also makes it easy to prove correctness.
- Cons: May perform sub-problems more than once. Often requires lots of branching in the code, which is typically slow.
Bottom-up: Solve all the sub-problems first, then use them to solve the super-problems.
- Pros: Can be faster because less decision-making and less branching.
- Cons: More difficult to conceptualize and prove correctness because it is generally the reverse of the recurrance relationship. May perform unnessary calculations on cases that are never used.

The above code sample is an example of a top-down approach to the problem.

Python quirk: In Python, there is a separate disadvantage to the top-down approach. Python limits the "recursion depth" (how many times a function can call itself, or another function in sequence) to a fixed number. In this problem, that would mean that the sum of the lengths of the two strings could not be longer than this maximum recursion depth.

Another Approach

If we didn't have to worry about how fast our algorithm ran, the top-down approach would be just fine. It's easy to understand and is easy to code. For small problems, we could stop right there and be perfectly happy...but we're never satisfied, are we? Let's see if another approach will ease the efficiency problems of our top-down approach, though be warned, we may be trading one set of problems for another!

Let's try solving all the sub-problems first, i.e. a bottom-up approach. But we need to keep track of the what we've solved so that we can use them in subsequent calculations. Since the sub-problems involve all possible sub-strings in all possible configurations, we need to find some way to easily represent all those possible combinations. ==> Matrices fit our design bill very well.

A matrix represents all possible combinations of one set of entities with another, creating a 2-dimensional space of all combinations.

So, one way to represent all the possible sub-problems is to create a matix, "D", that holds the results (minimum edit distances) for all the sub-problems where

D[i,j] is the edit distance between the substring of A of length i to the substring of B of length j.
String A is across rows and string B is across the columns, starting at position #1 (not 0!).
- Technically, each row or column position in the matrix represents the entire sub-string where the last character in the substring is the one currently being compared.
The first column and row, D[i,0] and D[0,j] represents the distance of the substrings to the empty string

Aside: One way to think of the first colum/row as of "padding" and empty string in front of the original strings. The technique of "padding" the A and B strings with a "dummy values is a very common technique in both mathematical proofs and numerical methods and can be found in diverse applications from computer graphics to quantum physics.

NOTE: This discussion uses the standard mathematical notation for matrix indexing, e.g. "D[i,j]". In Python code, since 2-D matrices can be represented as lists of lists, e.g. a 2x3 matrix could be D = [[0, 1, 2], [3, 4, 5]]. Indexing a value in the matrix would be written in Python as D[i][j].

Let's see how the recurrence relationships manifest themselves in this implementation:

Base cases:

The base case edit distance values are trivial to calculate: They are just the lengths of the sub-strings. We can just fill our matrix with those values using simple loops.

Inductive Cases:

The smallest edit distance between two strings has two possibilities, depending on the last characters in the two strings:

If the last characters are equal: The edit distance is the edit distance of the two substrings, both one character shorter then the current substrings, i.e. D[i,j] = 0+D[i-1,j-1]
If the last characters are not equal: The edit distance is one more edit than the edit distance of the smallest edit distance of any of the 3 possible substring situations, i.e. D[i,j] = 1 + min(D[i, j-1], D[i-1, j], D[i-1, j-1])

Notice is that for the inductive case, the sub-problem values that any spot in the matrix depends on are only to the left and above that point in the matrix (see the diagram below). That is, the edit distance value at any given point in the matrix does NOT depend on any values to its right or below it. This means that if we iterate throught the matrix from left to right and from top to bottom, we will always be iterating into positions in the matrix whose values only depend on values that we've already calculated!

The last element in the matrix, at the lower right corner, holds the edit distance for the entire source string being transformed into the entire target string, and thus, is our final answer to the whole problem.

Distance Matrix

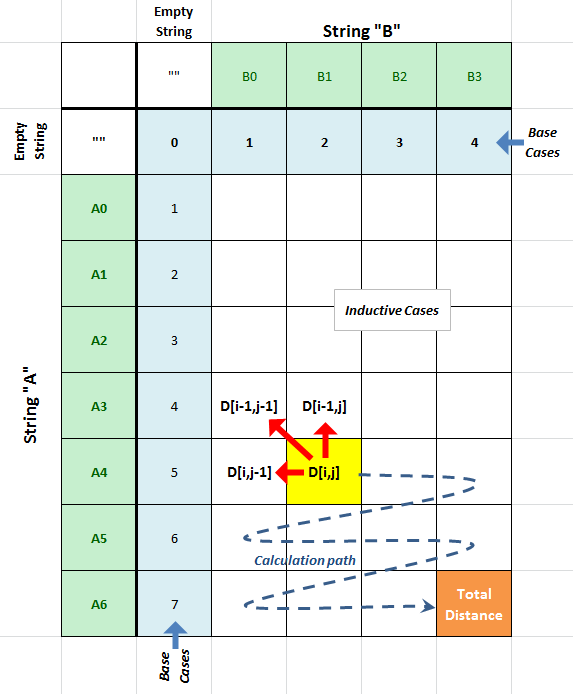
IMPORTANT: In the headers above, "Ai" and "Bj" refer to sub-strings of the A and B strings respectively, from their start up to and including the i'th/j'th character.

Question: Are there other interation paths through the matrix here that will satisfy the constraint of always working with previously calculated values? Is there an iteration path that will always work for any recurrence relationship?

Question: Are unnecessary calculations being performed here as well? Is the problem better or worse than the top-down approach?

Example: Transform "SPARTAN" into "PART"

The steps are

Step	Comparison	Edit necessary	Total Editing
1.	"S" to ""	delete: +1 edit	"S" to "" in 1 edit
2.	"P" to "P"	no edits necessary!	"SP" to "P" in 1 edit
3.	"A" to "A"	no edits necessary!	"SPA" to "PA" in 1 edit
4.	"R" to "R"	no edits necessary!	"SPAR" to "PAR" in 1 edit
5.	"T" to "T"	no edits necessary!	"SPART" to "PART" in 1 edit
6.	"A" to "T"	delete: +1 edit	"SPARTA" to "PART" in 2 edits
7.	"N" to "T"	delete: +1 edit	"SPARTAN" to "PART" in 3 edits

The red arrows in the diagram below show the dependencies of each edit distance value on its predecessors. The edit process described above is thus the reverse of that path.

Distance Matrix
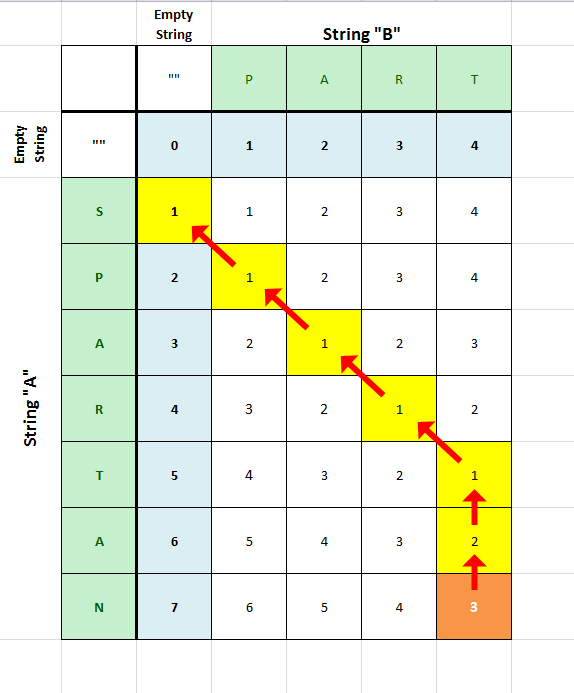
SPARTAN -> PART
Note: For clarity, the row and column headers are only the last letter in the relevant sub-string.

Example: Transform "PLASMA" into "ALTRUISM"

The steps are

Step	Comparison	Edit necessary	Total Editing
1.	"" to ""	no edits necessary!	"" to "" in 0 edits
2.	"P" to "A"	replace: +1 edit	"P" to "A" in 1 edit
3.	"L" to "L"	no edits necessary!	"PL" to "AL" in 1 edit
4.	"A" to "T"	replace: +1 edit	"PLA" to "ALT" in 2 edits
5.	"A" to "R"	insert: +1 edit	"PLA" to "ALTR" in 3 edits
6.	"A" to "U"	insert: +1 edit	"PLA" to "ALTRU" in 4 edits
7.	"A" to "I"	insert: +1 edit	"PLA" to "ALTRUI" in 5 edits
8.	"S" to "S"	no edits necessary!	"PLAS" to "ALTRUIS" in 5 edits
9.	"M" to "M"	no edits necessary!	"PLASM" to "ALTRUISM" in 5 edits
10.	"A" to "M"	delete: +1 edit	"PLASMA" to "ALTRUISM" in 6 edits

The above steps are shown as the yellow blocks below with the solid red arrows pointing in the opposite direction from the process above:

Distance Matrix
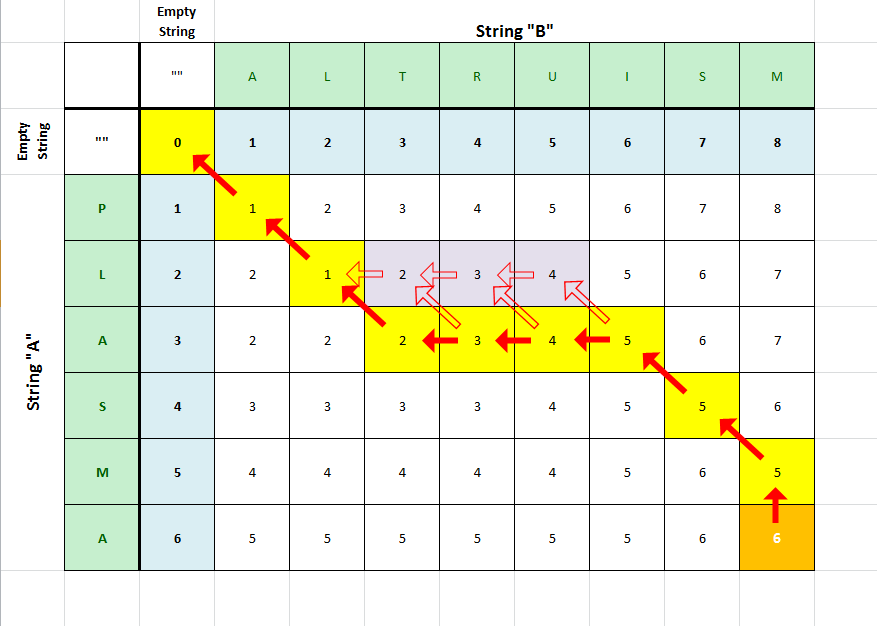
plasma to altruism example
Note: For clarity, the row and column headers are only the last letter in the relevant sub-string.

This example demonstrates that minimum edit paths are not unique, as shown with purple blocks and outlined arrows.

Pseudo-Code Implementation

We can easily construct a pseudo-code implementation of the above bottom-up algorithm from its description. This is a very useful intermediate step in creating code for an algorithm that many students neglect. Once the pseudo-code is complete, one only needs to translate it into actual Python code or whatever your favorite programming language happens to be.

The following is NOT valid Python code!

def edit_dist_matrix(a, b):
    """Generate the edit distance matrix for transforming string a into string b."""
    Create an empty len(a)+1 x len(b)+1 matrix ("d" below)
    Fill the matrix with the base case values
    Loop though each INDUCTIVE case row (sub-strings of a)
       Loop through each INDUCTIVE case column (sub-strings of b) 
           if the corresponding characters of a & b are the same (watch the indexing here!), d[i][j] = d[i-1][j-1] 
           else d[i][j] = 1 + the minimum of d[i, j-1], d[i-1][j], d[i-1][j-1]
    return the matrix
    
# The edit distance is the matrix's last element (bottom right cell) 
# Write a separate function to retrieve the final edit distance, given the two strings, a and b.

Implementation suggestions:

For any list in Python, aList[-1] is the last element of the list.
Write utility functions to make your initial, unfilled matix
- To make a list of nVals elements filled with a value, val, write: aList = [val]*nVals
  - Note that the foillowing code does NOT work properly because the exact same list, not a copy, is put in each row: aMatrix = [[val]*nCols]*nRows
  - You must use a loop or a list comprehension to create the rows of a matrix.

Here's a useful little function to print a 2-D matix nicely:

def print_matrix(m):
    """Print a 2-D matrix with each row on a different line."""
    for row in m:
        print row

In future courses, you'll see more examples of both top-down and bottom-up approaches, see how to distinguish when to use each approach, and also see a hybrid approach which (at least in theory) minimizes the calculational disadvantages.

COMP 130 Elements of Algorithms and Computation Spring 2012