1. Classes

Up until this point in the class, we have been using built in Python data structures to implement theoretical Computer Science constructs. For example, using a dict of sets to represent a graph. Further, we have also authored various functions, such as edge_count, that consume these representations and reveal specific properties about the instances they represent. Within the context of a specific program often such structures and functions embody a symbiotic like relationship — structures made to be passed to functions and functions made to accept structures — each being utilized nearly exclusively in the context of the other.

Object Oriented Programming (OOP, or sometimes just OO) is a style of program design built upon the philosophy that these context specific symbiotic relationships are so intrinsic to program construction that they deserve their own source level organization units. In OO terms, the marriage of these structures (data) and functions (behavior) is the class. Though it should be noted that when a function is included within a class we use the name method instead of function.

Classes go well beyond just gluing data and functions together and OOP also goes well beyond just classes. You will see much more in depth treatment of these ideas in COMP 215. We will not be asking you to create classes in 182. However, we will begin to start providing classes for your use as the course moves forward so it is worth spending a little time familiarizing you with some of their basic concepts.

The good news is that using classes should already be very familiar to you because we have been secretly utilizing them throughout lab. For example, both the dict and set entities in Python are in fact classes. One of the chief benefits of classes is that they provide separation of concern. For example, in the case of set, we have used this type frequently in lab to store integer elements. For example:

digits = set([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

Nowhere in this code do we instruct Python on how to store the digits or where to store the digits within the set, just that they should be stored in the set. Perhaps the set implementation stores them in a list or maybe a queue? As users of the set structure we actually have no idea how the set class is accomplishing its storage goal, just that it is accomplishing this goal. This is an example of one of the key aspects of classes, namely that they abstract from us implementation details. This is also true of methods within the class, for example union:

evens = set([0, 2, 4, 6, 8])
odds  = set([1, 3, 5, 7, 9])
digits = evens.union(odds)

How does union accomplish its task? What algorithm does it use? We actually have no clues based on our usage. And as users of a class we don't really care. As long as the given method performs its task in compliance with the related documentation our program will operate correctly.

This observation lends great power to class authors. Because the programs that use classes depend only on what is accomplished by the class and not how it is accomplished, the class author is free to change how their class works at will. For example, maybe in Python 2.6 union used a $O(n*m)$ algorithm but in Python 2.7 was improved to $O(n*log(m))$. This change can be seamlessly made behind the scenes without breaking the existing programs that use set.

Another feature of classes is encapsulation. Notice how once a set is created in Python our only options for adding or removing elements to/from the set is by means of invoking its methods. For example add or remove. We have no direct access to the data within the class itself — we must go through one of the approved set methods to change the contents of the set. This aspect, namely encapsulation, ensures that the set representation is accessed in a consistent and predictable manner which in turn helps ensure program correctness.

This also allows us to write complex functionality once, encapsulate it, and use it over and over. This is good program design. You hide the complex behavior, test it thoroughly, then you and everyone else using the class benefits. Contrast this to a situation where you do not encapsulate that functionality. If you need to re-implement complex behaviors every time you need them, you have to invest significant effort writing and testing that code. It is far more likely that you will make a mistake and waste precious time.

2. Recursive Structures and Algorithms

Useful definitions:

Binary Tree: A tree where each node has 0, 1, or 2 children.

Full Binary Tree: A binary tree where each node has 0 or 2 children.

Complete Binary Tree: A binary tree in which every level, except possibly the deepest, is completely filled. At depth n, the height of the tree, all nodes must be as far left as possible. (NIST definition)

A recursive structure is a structure that is composed of itself.

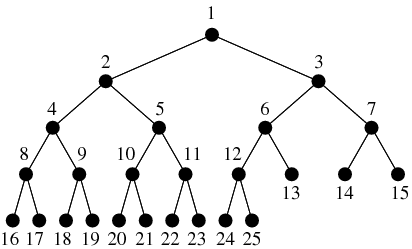
(source: Weisstein, Eric W. "Complete Binary Tree." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CompleteBinaryTree.html)

Consider then the class FullBiTree.py which we have provided. To create a FullBiTree we call a special method of the class called the constructor which has the same name as the class itself:

>>> import FullBiTree
>>> leaf1 = FullBiTree.FullBiTree("Leaf 1")
>>> leaf2 = FullBiTree.FullBiTree("Leaf 2")
>>> root = FullBiTree.FullBiTree("R", leaf1, leaf2)
>>> print root
Root(Leaf 1, Leaf 2)

Note how when we create root we provide two FullBiTree instances as the left and right subtrees to root. Since our FullBiTree class is composed of other FullBiTrees it is a recursive implementation of full binary trees.

The advantage of recursive structures is that they lend themselves well to recursive algorithms, which we have seen previously. As such we can use recursion to quickly and elegantly solve a host of tree related problems that might otherwise have awkward non-recursive solutions. For example, consider the problem of counting the number of leaves in a full binary tree when the tree is represented as a dict and as our FullBiTree:

def count_leaves_full_bitree_dict(tree):
    """
    Counts the number of leaves in a tree in dict form.
    """
    num_leaves = 0
    for adj_set in tree.values():
        adj_set_size = len(adj_set)
        if adj_set_size == 0:
            num_leaves += 1

    return num_leaves

def count_leaves_fullbitree(tree):
    """
    Counts the number of leaves in a FullBiTree.
    """
    ...

For reference, here are all of the available methods of FullBiTree:

    def get_name(self):
        """
        Gets the name of the root node of the tree.

        Returns:
        The name of the root node.
        """
        return self.__name

    def get_left_child(self): 
        """ 
        Gets the left subtree of the tree's
        root if it has children or generates an exception if the root
        has no children.

        Returns:
        The left subtree of the tree.
        """
        return self.__get_state().get_left_child()


    def get_right_child(self):
        """
        Gets the right subtree of the tree's root if it has children 
        or generates an exception if the root has no children.

        Returns:
        The left subtree of the tree.
        """
        return self.__get_state().get_right_child()


    def set_children(self,left_tree, right_tree):
        """
        Updates the tree's root to contain new children.

        Arguments:
        left_tree - the new left subtree for the tree.
        right_tree - the new right subtree for the tree.
        """
        self.__set_state(TreeNodeStateInternal(left_tree, right_tree))


    def remove_children(self):
        """
        Updates the tree's root to contain no children.

        Arguments:
        left_tree - the new left subtree for the tree.
        right_tree - the new right subtree for the tree.
        """
        self.__set_state(TreeNodeStateLeaf())

    def is_leaf(self):
        """
        Tests whether the tree's root has no children.

        Returns:
        True if the tree is only a single node, else false.
        """
        return self.__get_state().is_leaf()

    def get_node_property(self, key):
        """
        Accesses a user specified property of the tree's root.

        Arguments:
        key - the property of the desired key value pair.

        Returns:
        The value of the given key for the tree's root.
        """
        return self.__node_props[key]


    def set_node_property(self, key, value):
        """
        Defines a user specified property of the tree's root.

        Arguments:
        key - the key of the desired property.
        value - the value of the desired property.
        """
        self.__node_props[key] = value

    def get_left_edge_property(self, key):
        """
        Accesses a user specified property of the tree's left subtree edge.
        Throws exception if the tree has no left subtree.

        Arguments:
        key - the property of the desired key value pair.

        Returns:
        The value of the given key for the tree's left subtree edge.
        """
        return self.__get_state().get_left_edge_property(key)

    def set_left_edge_property(self, key, value):
        """
        Defines a user specified property of the tree's left subtree edge.
        Throws exception if the tree has no left subtree.

        Arguments:
        key - the key of the desired property.
        value - the value of the desired property.
        """
        self.__get_state().set_left_edge_property(key, value)


    def get_right_edge_property(self, key):
        """
        Accesses a user specified property of the tree's right subtree edge.
        Throws exception if the tree has no left subtree.

        Arguments:
        key - the property of the desired key value pair.

        Returns:
        The value of the given key for the tree's right subtree edge.
        """
        return self.__get_state().get_right_edge_property(key)


    def set_right_edge_property(self, key, value):
        """
        Defines a user specified property of the tree's right subtree edge.
        Throws exception if the tree has no left subtree.

        Arguments:
        key - the key of the desired property.
        value - the value of the desired property.
        """
        self.__get_state().set_right_edge_property(key, value)

Exercise 2.1: Tree Height

The height of a tree is defined to be the length of the longest path from the root to any leaf. Write a function:

def tree_height(tree):
    """
    Computes the hight of a FullBiTree.

    Arguments:
    tree - a full binary tree in FullBiTree form.

    Returns:
    The height of the tree
    """

to compute the height of a FullBiTree.

Assert that:

>>> tree_height(FullBiTree.FullBiTree("Z"))
0

and

>>> r = FullBiTree.FullBiTree("R", FullBiTree.FullBiTree("A", FullBiTree.FullBiTree("C"), FullBiTree.FullBiTree("D")), FullBiTree.FullBiTree("X"))
>>> tree_height(r)
2

2.2 Infix Order

The infix order string of a tree is a string listing of a tree's nodes where, for every given node, all the nodes left of the given node in the string are in the left subtree of the given node and all nodes right of the given node in the string are in the right subtree of the given node. For example the infix order string of:

FullBiTree.FullBiTree("R", FullBiTree.FullBiTree("A", FullBiTree.FullBiTree("C"), FullBiTree.FullBiTree("D")), FullBiTree.FullBiTree("X"))

is

CADRX

Write the function:

def infix_string(tree):
    """
    Computes the infix order string of a tree.

    Arguments:
    tree - a full binary tree in FullBiTree form.

    Returns:
    An infix string of the tree.
    """

and assert that:

infix_string(FullBiTree.FullBiTree("R", FullBiTree.FullBiTree("A", FullBiTree.FullBiTree("C"), FullBiTree.FullBiTree("D")), FullBiTree.FullBiTree("X")))

is

CADRX

2.3 Paths from Root to Leaves.

Write a function to find and record all paths in a given FullBiTree starting at the root and terminating at each leaf. Feel free to use helper functions if needed.

def find_paths(tree):
    """
    Computes a string for each path in the given tree starting at the root and terminating at a leaf.

    Arguments:
    tree - a FullBiTree

    Returns:
    A set of strings encoding the order of nodes in each path from the root to all leaves.
    """

and assert that:

find_paths(FullBiTree.FullBiTree("R", FullBiTree.FullBiTree("A", FullBiTree.FullBiTree("C"), 
           FullBiTree.FullBiTree("D")), FullBiTree.FullBiTree("X")))

is

set(['RAD', 'RX', 'RAC'])

2.4 BST Property

A binary tree is said to have the binary search tree property iff for every node n in the tree all left descendants of n have a value less than or equal to the the value of n and all right descendants of n have a value greater than or equal to the value of n. Given a FullBiTree where the name of each node is an integer, write a function to test whether a given tree has the BST property:

def is_valid_bst(tree):
    """
    Tests to see if the given tree has the binary search property.

    Arguments:
    tree - a FullBiTree where the value of each node is an integer stored as the node's name.

    Returns:
    True if the tree has the binary search property, else false.
    """
    ...

Determine whether the following trees have the binary search property:

tree1 = FullBiTree.FullBiTree(50, FullBiTree.FullBiTree(25, FullBiTree.FullBiTree(15), FullBiTree.FullBiTree(35)), 
                              FullBiTree.FullBiTree(75, FullBiTree.FullBiTree(60), FullBiTree.FullBiTree(90)))
tree2 = FullBiTree.FullBiTree(50, FullBiTree.FullBiTree(25, FullBiTree.FullBiTree(15), FullBiTree.FullBiTree(35)), 
                              FullBiTree.FullBiTree(75, FullBiTree.FullBiTree(60), FullBiTree.FullBiTree(9)))
tree3 = FullBiTree.FullBiTree(50, FullBiTree.FullBiTree(25, FullBiTree.FullBiTree(15), FullBiTree.FullBiTree(100)), 
                              FullBiTree.FullBiTree(75, FullBiTree.FullBiTree(60), FullBiTree.FullBiTree(90)))

Submit your code

At the end of lab, submit your group's Python code here.

3. Reference Material

You may find the collections.Counter container useful for the current assignment. It allows you to easily count unique items in a sequence, such as a string. For example:

>>> import collections
>>> count = collections.Counter('abcdabcaba')
>>> count
Counter({'a': 4, 'b': 3, 'c': 2, 'd': 1})
>>>

Be sure to read the documentation to better understand how you might use these counters.

COMP 182 Lab 7