In programming, it is often necessary to have objects with which one can store data, retrieve data when needed, and remove data when no longer needed.  Such objects are instances of what we call container classes.  There are basically two schemes for organizing the objects for storage: a linear scheme and a non-linear scheme.  This leads to the notion of container structures.  The linear container structure is called a list.  The non-linear structure can be sub-classified into many sub-types such as the various tree structures and hash tables.  

This lecture focuses on the list structure, its implementation and the structure of algorithms that process lists.

Going Shopping

Before I go to the groceries store, I make a list of what I want to buy.  Note how I build my shopping list: I start with a blank sheet of paper, then I add one item at a time.

When I get to the store, I start buying things by going down my list.  For each item I buy, I mark it off the list.

After I am done shopping, I go to the cashier and check out my items.

The cashier scans my items one item at a time.  Each time, the cash register prints one line showing the item just scanned together with its price.  Again, note how the cash register builds the list: it start with a blank sheet of paper and then add one item at a time.  After all items have been scanned, the cashier press a key and "poof", the cash register prints a subtotal, then a tax amount for all the taxable items, then a total amount, and finally a total number of items bought.

At different store, the cash register not only prints out all of the above, but also a total amount of "savings" due to the fact that I have a "member-plus" card.  Some other stores don't care to print the total number of items bought at all.  Whatever the store, wherever I go, I see "lists" and "list processing" all over.

The check out cash register uses a program to enter the items and print the receipt.  At the heart of the program is a container structure to hold data (data structure) and a few algorithms to manipulate the structure and the data it holds.  The simplest way to organize data is to structure them in a linear fashion; that is, intuitively, if we can get hold of one data element, then there is exactly one way to get to the next element, if any.  We can this linear organization of data the list structure.  Before we can do any list processing, it is imperative that we articulate more clearly what a list is.

What is a list?

Analogous to the notion of a shape, a list is an abstract notion.  Recall how I built my list of groceries items?  I started with a blank list: an empty list!  The empty set!  

An empty list is a list that has no element.

It is obvious that there are non-empty lists.  But what do we mean by a non-empty list?  How can we articulate such an obvious notion?  Consider for example the following list consisting of three elements.

• milk
• bread
• butter

In the above, we organize the items in a linear fashion with milk being the first element, bread being the next element following bread and butter being the next element following bread.  Is there any item that follows butter?

Is

• bread
• butter

a list?

Is

• butter

a list?

Is there a  list that follows butter in the above?

A non-empty list is a list that has an element called first and a list called rest.

Note that in the above formulation, the rest of a list is itself a list!  The definition of a list is what we called a recursive definition.  The list contains a substructure that is isomorphic to itself.

The Composite Design Pattern

The UML diagram below captures the recursive data definition of the list data structure.

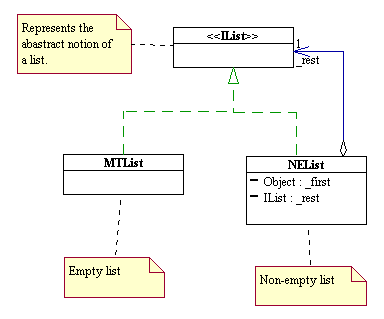
This definition translates into Java code as follows.

/**
 * Represents the abstract list structure.
 */
public interface IList {
}

/**
 * Represents empty lists.
 */
public class MTList implements IList {
}

/**
 * Represents non-empty lists.
 */
public class NEList implements IList {
   private Object _first;
   private IList _rest;
}

The above is an example of what is called the composite design pattern.  The composite pattern is a structural pattern that prescribes how to build a container object that is composed of other objects whose structure is isomorphic to that of the container itself.  In this pattern, the container is called a composite. In the above, IList is called the abstract component, MTList is called the basic component and NEList is called the composite.  The composite design pattern embodies the ,concept of recursion, one of the most powerful thinking tool in computing.  (There is a subject in theoretical computer science and mathematics called "recursive function theory," which the studies the meaning of what computing means and in effect defines in the most abstract form what a computer is and what it can do.)

Now that we have defined what a list is, we ask ourselves how we can process it?  What can we do with a list?  The above code makes it clear that there is not a whole lot we can do with a list besides instantiating a bunch of MTList objects vie the call new MTList() (why?).  The list is completely encapsulated, that is all internal components (if any) of a list  are private and cannot be accessed by any external code.  The right question to ask is "what can a list do for us?"

Abstract Computation on The Composite Structure and The Interpreter Design Pattern

What can a list do?

Length of a list

Suppose we are given a list L and asked to find out how many elements it has.  What should we do?  The temptation here is to start thinking about "traversing" the list and keep a count as we go along, and when we encounter the "end" of the list, the count should be the number of elements in the list. But how do we know that that's the right answer?  In order to determine whether or not the result obtained by counting as one traverses the list from beginning to end is correct, we have to define what it means to be the number of elements in the list.  The number of elements in a list is an abstract notion, isn't it?  In order to define such a quantity, we need to go back to the definition of what a list is.

• A list is an abstract notion of a container structure.
• An empty list is a list that has no element
• A non-empty list is a list that has an element called first and a list called rest.

To define the notion of the number of elements in a list, we need to define what we mean by the number of elements in an empty list and what we mean by the number of elements in a non-empty list.

• The number of elements of an empty list is 0.
• The number of elements in a non-empty list that contains first and rest, is 1 plus the number of elements in rest.

The definition of the number of elements in a list is thus recursive.  Which ever approach we use to compute the number of elements in a list, in order to prove correctness, we must show that the result satisfies the above definition.

Here is the code for the above computation.

package listFW;

/**
 * Represents the abstract list structure.
 */
public interface IList {
    /**
     * Abstract notion of the number of elements in this IList.
     */
    int getLength();
}

package listFW;

/**
 * Represents empty lists.
 */
public class MTList implements IList {
    /**
     * The number of elements in an empty list is zero.
     */
    public int getLength() {
        return 0;
    }
}

package listFW;

/**
 * Represents non-empty lists.
 */
public class NEList implements IList {
   private Object _first;
   private IList _rest;

   // Constructor ommitted.

   /**
    * The number of elements in a non-empty list is 
    * the number of elements of its rest plus 1.
    */
   public int getLength() {
       return 1 + _rest.getLength();
   }
}

Last Revised Thursday, 03-Jun-2010 09:50:06 CDT

©2004 Stephen Wong and Dung Nguyen