
|
|
Comp202: Principles of Object-Oriented Programming II
|
Fundamentally the idea here is to insert known team objects (supplied as the input parameter) into a binary tree (BiTree). The known team objects should end up in "leaf" nodes in the tree. That is, the nodes they are in always have null trees as the sub-trees. A known team's "opponent" is the team held as the root data of the team's sibling tree. The interior (non-empty, non-leaf) nodes should always contain unknown teams.
Note that this does not preclude teams from having "bye's". In fact, this capability will insure that a team never has a null tree as an opponent. Thus if a team is inserted into empty tree, the team will be attached as the root data right there. But when the tree being inserted into is non-empty, thre are two possibilities.
To help us figure out what to do when, we will create a "process flow diagram". A process flow diagram traces the program execution as it travels through a data structure. At every point there may be several cases to consider, each with different resulting actions. As we saw in the Koch curve project, an OO system "gets the job done" by delegating from one object to the next until an unequivocal statement of what needs to be done can be made. At every dispatch, a little more is learned about the system, until finally, enough information has been accrued that the correct action can be taken. Process flow diagramming is a technique whose utility is not limited to OO systems. If one were to solve the problem using procedural programming techniques, a process flow diagram is also the correct way to start. This is because it helps formalize the whole process and because it clearly identifies each case encountered, it makes sure that there are no "holes" in the algorithm, creating more robust code.
Below, I have diagrammed out the process flow for the InsertTeamAlgo we need.
To intepret the diagram below:
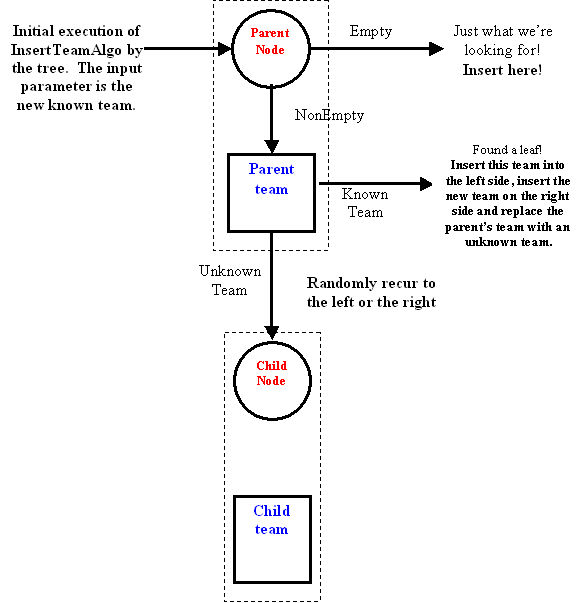
Spend some time convincing yourself that the above process will correctly form the tournament tree.
The next step is to lay the above process in a more tabular form with each case and indented sub-cases:
Empty case: Insert here!
NonEmpty case: Delegate to the team in the root data.
Known team case: Should be a leaf so insert the this team object into the left child tree (how do you insert a team into a tree?). Insert param into the right child tree. Replace the rootDat with an unknown team.
Unknown team case: No leaf or end-point yet. Randomly pick the left or right sub-tree and recur into it.
You should be able to write the code directly from the above description using an IVisitor-derived class with one anonymous inner class. Don't forget to make input parameters final if they are to be accessed by an inner class!
Note that there is no notion of "checking" in the above process. The nodes and data are the object that they are, which may be one of several possibilities. The actions take place due to the object being the type that it is--no checking or conditionals are required or allowed, except in the random direction choosing!
The InsertTeamAlgo assumes that the tree is in proper tournament form. What happens if, for some reason, the tree is incorrectly formed when the InsertTeamAlgo is executed? Can you create a tree such that your code to throws an exception? If so, can you modify your code so that your code won't throw an exception, even for very badly formed trees? In fact, if done correctly, the InsertTeamAlgo should progressively repair any damage in the tree as each new team is inserted. (Try this on the demo: Create a tournament and play a round or two. Now insert some new teams. Watch how the structure slowly returns to having all the teams back on the leaves! -- Note that some names will appear twice because they were in the tree twice to begin with.) Now that's robustness!
Last Revised Thursday, 03-Jun-2010 09:52:23 CDT
©2006 Stephen Wong and Dung Nguyen