|
|
Comp202: Principles of Object-Oriented Programming II
Fall 2007 -- Design
Patterns for Self-Balancing Trees
|
- Introduction to run-time cost analysis: "Big-Oh"
notation. See below.
- Why do we need balanced trees?
- Trees offer much faster access than lists, but only
if the tree so long as all the branches are nearly the same length, i.e.
"balanced".
- A balanced tree gives O(log n) behavior, while lists
give O(n) behavior.
- Worst case scenario for an unbalanced tree is O(n)
behavior.
- Demo code
- Pre-Java 5.0 JRE/SDK:
- binaries in a jar
file (To run: java -jar
NTree.jar)
- source code, zipped
- Java 5.0-compatible JRE/SDK
- DrJava project
- Executable jar
file (To run: java -jar
dp4sbt_jre50.jar)
- Using generics and lambda-based extended visitors
- Executable jar file
- Source code, includes both
lambda-based and case-statement based generic code.
- PowerPoint Presentationn
- OOPSLA 2002
materials
- Paper in PDF format
- Poster (>740KB PNG file!)
Accounting For The Resources Used By Computations:
"Big-Oh" notation
- A running program consumes resources such as time (seconds) and space
(bits). Frequently, we abstract our units, and measure steps and objects,
instead of seconds and bits.
- When comparing programs (or algorithms), you should first pay
attention to gross differences in time or space consumed, for
example, n^3 versus n^2 steps, rather than 3n versus 2n
steps.
- For a few programs, the cost is fixed and can be calculated by examining
the program text. More frequently, however, cost depends on characteristics
of the input, such as length.
- When we make gross comparisons of programs, we often refer to the
``order-of-magnitude'' of the cost. The notation used is sometimes called
``Big-Oh,'' and is always of the form O(f(n)) where f(n) is
some function over the positive integers.
- The Big-Oh notation simply means that the cost function is bounded by
(is less than) some multiple of the function f(n). For example, if
we say
we mean that P equals n^3, plus some terms that are ``on the order of
n^2''---i.e., they don't grow faster than kn^2, where k
is some constant term.
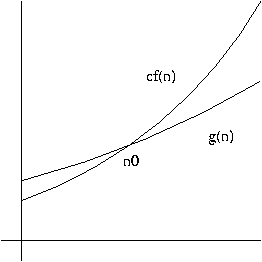
- Here are some equivalences that allow you to manipulate equations
involving order-of-magnitude quantities:
- f(n) = O(f(n))
- K * O(f(n)) = O(f(n))
- O(f(n)) + O(f(n)) = O(f(n))
- O(f(n)) * O(g(n)) = O(f(n) * g(n))
- Also, the base to which a logarithm is computed doesn't affect the order
of magnitude, because changing the base of the logarithm from 2 to c
changes the value by a constant factor of log2(c).
(written by Alan Cox)
Quick and Dirty Explanation:
Big-Oh tells us how a cost of running a program
(algorithm) scales with respect to n for large values of n, e.g. linearly,
quadraticly, logarithmically, etc. The slower the cost rises with n,
the better, so long as we are dealing with large values of n.
Examples:
- Summing a list of numbers: O(n) -- single
traversal of the list
- Sorting a list by inserting first into a sorted rest:
O(n^2) -- double traversal of the list (a traversal to insert each
element)
- Finding an element in a perfectly balanced binary
search tree: O(log(n)) -- height of a balanced tree is O(lon(n))
- Finding an element is a completely unbalanced tree,
worst case scenario: O(n) -- all elements along one branch =
linear structure.
Last Revised
Thursday, 03-Jun-2010 09:52:34 CDT
©2007 Stephen Wong and Dung Nguyen

