Exam #1 - Comp 212

Rice University - Fall 2000

1. The examination is closed book/notes.
2. Fill in your name on every page of the exam.
3. Fill in and sign the honor pledge below.
4. If you forget the name of a Java class or method, make up a name for it and write a brief explanation in the margin.
5. You will not be penalized on syntax errors, but do try to write Java code as syntactically correct as possible.
6. Write your code in the most object-oriented way possible, that is with the fewest number of control statements and no checking of the states and class types of the objects involved.
7. In all of the questions, feel free to write additional helper methods or visitors to get the job done.
8. Make sure you use the Singleton pattern whenever appropriate. Unless specified otherwise, you do not need to write any code for it. Just write "singleton pattern" as a comment.
9. For each algorithm you are asked to write, 90% of the grade will be for correctness , and 10% will be for efficiency and code clarity.
10. There are 6 questions for a total of 100 points.
11. You have two hours to complete the exam.

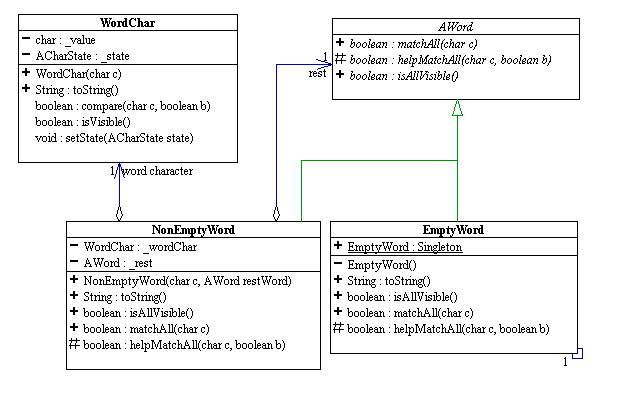
In milestone 1 of the hangman project, you are asked to implement AWord as shown in the following UML diagram.

1. Describe how you would implement AWord using the visitor pattern as well by drawing an appropriate UML diagram showing only the public methods of all the classes involved.  Explain briefly the rationale for each of the abstract public methods in AWord.  Describe briefly each of the concrete visitors you must have.  Do not write any code.  20 points

Polynomials

A polynomial of one variable, p(x),  is an expression of the form

a_nxⁿ + a_n-1x^n-1+ ... + a₁x + a₀,

where n is a non-negative integer, a_k  (k = 0.. n) are numbers, and a_n is a number not equal to 0. 

n is called the degree (or order) of p(x),a_k  (k = 0.. n) are called the coefficients of p(x), and a_n is called the leading coefficient of p(x). 

For examples:

• p(x) = 12x⁵ - 3x² + 7 is a polynomial of degree (order) 5 with leading coefficient 12.  -3x² + 7 is called the lower order polynomial for p(x).
• p(x) = 7 is a polynomial of degree 0 with leading coefficient 7.   This is an example of a constant polynomial.  It has no lower order polynomial.

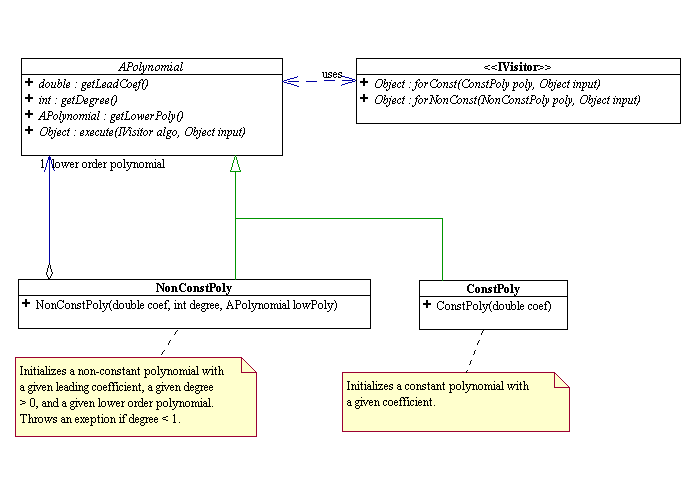
We can describe polynomials  in the following manner.  There is an abstraction called polynomial.  A constant polynomial is a polynomial with a leading coefficient and degree (order) 0.  A non-constant polynomial is a polynomial with a leading coefficient, a non-zero degree, and a lower order polynomial.  The polynomial's intrinsic behavior is to provide the clients with its degree -getDegree (), its leading coefficient - get LeadCoef (), and its lower order polynomial (if any) - getLowerPoly ().  Polynomials can be viewed as having an immutable linear recursive structure and can be implemented using the composite pattern.  All extrinsic algorithms on polynomials can be implemented as visitors to polynomials.  The following UML diagram illustrates the design of the polynomials and their visitors.  In this diagram, all the inherited concrete methods are not shown in order to save space.

2. Write a polynomial visitor called ToString to compute and return the String representation of the host as described by the following.  For constant polynomials, return the String representation of the coefficient (you may use Double.toString (double d) to convert a double to a String).  For non-constant polynomials, use ^ to denote exponentiation, and if the constant term is zero, do not show zero.  For examples, 12x⁵ - 3x² + 7 prints as 12x^5 + -3x^2 + 7, and 12x⁵ - 3x² + 0 prints as 12x^5 + -3x^2.   15 points

3. Write a polynomial visitor called AddConst to add a constant double to the host polynomial and return the resulting polynomial.  Decide how to pass the constant to AddConst yourself.  10 points

4. Write a polynomial visitor called Add to add a polynomial to the host and return the resulting sum polynomial.  Decide how to pass the polynomial parameter to Add yourself.  Feel free to use the AddConst visitor in the previous question to facilitate the coding.  15 points

Linear Recursive Structures

5. Write a visitor for an AListFW called LastNElements to compute and return an AListFW that contains the last n elements of the host.  Here 0 <= n, and the case n equals 0 corresponds to the empty list.  When n is more than the number of elements in the list, throw an appropriate exception.   Decide how to pass n to LastNElements yourself.  20 points

6. Write a visitor for an LRStruct called TruncateN to truncate the host and keep only the first n elements of the host.  Here 0 <= n, and the case n equals 0 corresponds to the empty list.  When n is more than the number of elements in the list, the host should remain unchanged.   Decide how to pass n to TruncateN yourself.  20 points