2-3-4 Tree
Definition
A 2-3-4 tree is a container of data that can be compared by a total ordering relation.
For the sake of definiteness, we can assume without loss of generality that the
data in concern are integers. A 2-3-4 tree can be empty or not empty.
- When it is empty, it contains no data elements. We denote an empty 2-3-4 tree by
[].
- When it not empty, it can be in one of the following states: 2-state, 3-state, and
4-state.
- When it is in the 2-state, it contains one data element, N, and two 2-3-4 trees called
the left subtree (lst) and the right subtree (rst). All the
elements in lst are less than N, and all elements in rst are greater
than N. We denote a 2-state tree by [lst, N, rst].
- When it is in the 3-state, it contains two data elements, N1 and N2, and three 2-3-4
trees called the left subtree (lst), the middle subtree (mst), and the
right subtree (rst). N1 is less than N2. All the elements in lst
are less than N1. All elements in mst are greater than N1 and less than N2,
and all elements in rst are greater than N2. We denote a 3-state tree by [lst,
N1, mst, N2, rst].
- When it is in the 4-state, it contains three data elements, N1, N2 , and N3, and four
2-3-4 trees called the left subtree (lst), the middle-left subtree (mlst),
the middle-right subtree (mrst), and the right subtree (rst). N1
is less than N2, and N2 is less than N3. All the elements in lst are less
than N1. All elements in mlst are greater than N1 and less than N2.
All elements in the mrst are greater than N2 and less than N3, and all elements
in rst are greater than N3. We denote a 4-state tree by [lst, N1,mlst,
N2, mrst, N3, rst].
Self-balancing Tree
Starting from an empty 2-3-4 tree, we want to be able to add elements to the tree in
such a way that not only the 2-3-4 tree property is maintained but also all the subtrees
at the same level are balanced, i.e. have the same height. This balance property
permits a O(logN) lookup operation, where N is the number of elements in the tree.
The following insertion algorithm achieves this goal.
Insertion Algorithm
Let T be a 2-3-4 tree. The main idea behind inserting an integer
N into T is as follow: go down the search path for N in the tree, and insert it into the
appropriate leaf; along the search path, if a 4-state tree is encountered, split it into a
2-state tree and merge it with its parent tree (if any) before inserting N. The insertion
of N into T involves the following cases.
- The empty case: T changes to a 2-state tree containing N, an empty left
subtree and an empty right subtree.
- The 2-state case: [lst, X, rst]
- If T is a leaf, then T changes to a 3-state tree containing N and X in
the proper order, with all empty subtrees.
- If T is not a leaf, then N is inserted into lst when N < X,
N is inserted into rst when X < N.
- The 3-state case: [lst, X, mst, Y, rst]
- If T is a leaf, then T changes to a 4-state tree containing N, X, and Y
in the proper order, with all empty subtrees.
- If T is not a leaf, then N is inserted into lst when N < X,
N is inserted into mst when X < N < Y, and N is inserted into rst
when Y < N.
- The 4-state case: [lst, X, mlst, Y, mrst, Z, rst]
- If T is an orphan, then T splits in the following way before
N is inserted. T changes to the 2-state tree [[lst, X, mlst], Y, [mrst,
Z, rst]]. After such a split, N is inserted in T.
- T has a parent tree, say P, then T merges with its parent tree in the
following way before N is inserted. As we consistently split all
4-state trees on the way down the tree, the parent tree, P, can only be a 2-state tree or
a 3-state tree.
- Case P is a 2-state tree:
- If P = [p-lst, M, T], then P becomes [p-lst, M, [lst,
X, mlst], Y, [mrst, Z, rst]].
- If P = [T, M, p-rst], then P becomes [[lst, X, mlst],
Y, [mrst, Z, rst], M, p-rst].
- Case P is 3-state tree:
- If P = [p-lst, M1, p-mst, M2, T], then P becomes [p-lst,
M1, p-mst, M2, [lst, X, mlst], Y, [mrst, Z, rst]].
- If P = [p-lst, M1, T, M2, p-rst], then P becomes [p-lst,
M1,[lst, X, mlst], Y, [mrst, Z, rst], M2, p-rst].
- If P = [T, M1, p-mst, M2, p-rst], then P
becomes [[lst, X, mlst], Y, [mrst, Z, rst], M1, p-mst,
M2, p-rst].
After such a merge, N is inserted in [lst, X, mlst]
if N < Y, otherwise N is inserted in [mrst, Z, rst].
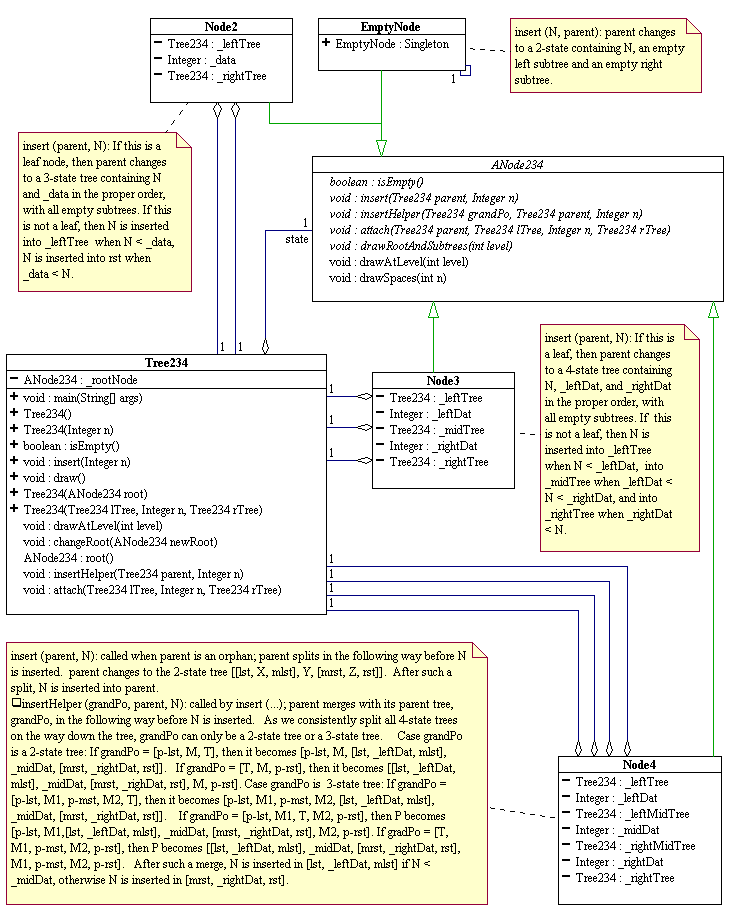
The 2-3-4 tree with the above insertion algorithm can be implemented
using the state pattern as shown in the following UML diagram.
Author: Dung X. Nguyen
Copyright 1999 - All rights reserved.

