| Pledge of Honor |
| 1. ( 18 pts) | 2 a) (8 pts) | 2 b) (8 pts) | 2 c) (8 pts) | 3. (18 pts) | 4 a) (5 pts) | 4 b) (15 pts) | 5 a) (10 pts) | 5 b) (10 pts) | Total (100) |
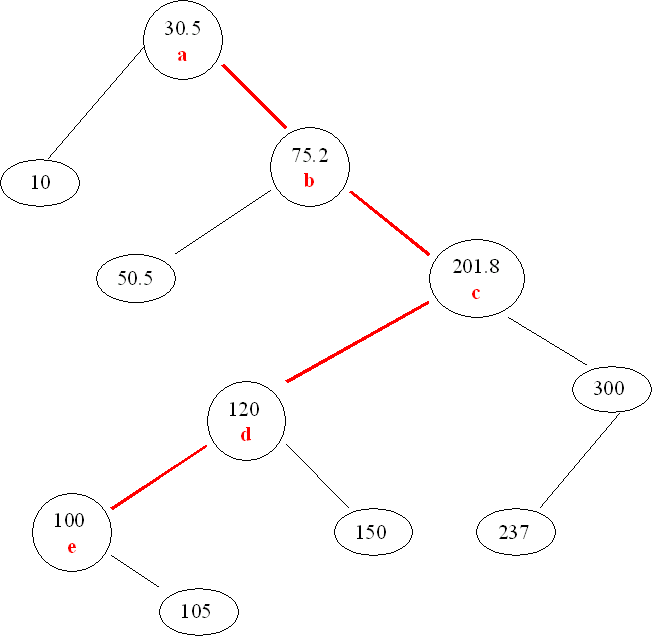
1. Write a BiTree visitor, called RemGreaterThan, for execution on a binary search tree (BST) that removes all objects greater than a given key, transferring them to a new BiTree. The key is passed as a parameter to the visitor. The new BiTree is returned by the visitor. This new BiTree must be a BST. Finally, to receive full credit, your visitor must visit the fewest possible nodes. For example, in the BST shown below, only the nodes a, b, c, d, e should be visited. when removing elements greater than 99.

2. a) Write a BiTree visitor, called FindIthLargest, that finds the i-th largest node assuming that the BiTree is a binary search tree (BST) and returns the subtree that contains this node at the root. The Integer index, i, is passed to the visitor as a parameter. The 0-th index corresponds to the first largest node. Throw an exception if the given tree is empty or if i is greater than the number of nodes in the tree.
b) Now, assume that each node of the BiTree is augmented with its weight. A node's weight is simply the number of non-empty nodes contained within the BiTree rooted at the node. An empty node has weight 0. See the illustration below.
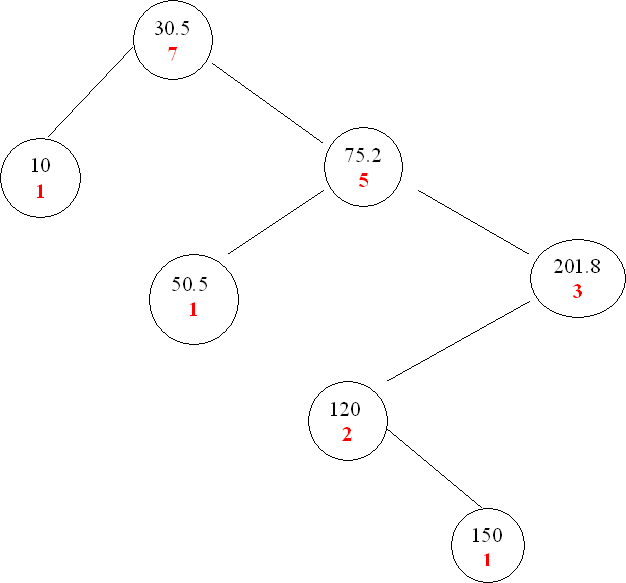
The root data element of a non-empty BiTree is now a pair defined by:
public class DatWeightPair {
private Object _dat;
private int _weight;
public DatWeightPair(Object d, int w) {
_dat = d;
_weight = w;
}
public Object getDat() {
return _dat;
}
public int getWeight() {
return _weight;
}
public void setDat(Object d) {
_dat = d;
}
public void setWeight(int w) {
_weight = w;
}
}
Revise your visitor from part (a) to take advantage of the weights to reduce the number of nodes visited.
Note: To receive full credit, never ask a subtree its weight. Instead, solve this problem in the same style as the BiTree visitor
that determined if a BiTree is a leaf.
c) Here is the code for the binary search tree insertion algorithm,
BSTInserter, given in the lecture. Revise the BSTInserter visitor to maintain the weights.
public class BSTInserter implements IVisitor {
private Comparator _order;
public BSTInserter (Comparator order) {
_order = order;
}
public Object emptyCase(BiTree host, Object input) {
host.insertRoot (input);
return host;
}
public Object nonEmptyCase(BiTree host, Object input) {
Object root = host.getRootDat();
if (_order.compare(input, root) <
0) {
return
host.getLeftSubTree().execute(this, input);
}
if (_order.compare(input, root) >
0) {
return
host.getRightSubTree().execute(this, input);
}
host.setRootDat(input);
return host;
}
}
3. Write an LRStruct visitor to remove the median. Assume the LRStruct contains Integers sorted in increasing order. Throw an exception when the LRStruct is empty. Do this with minimal traversal of the list structure. The median of a sorted list of N (N > 0) elements is the element at the index N/2. The first element has index 0.
4. Consider the following design for a restricted access container (RAC):
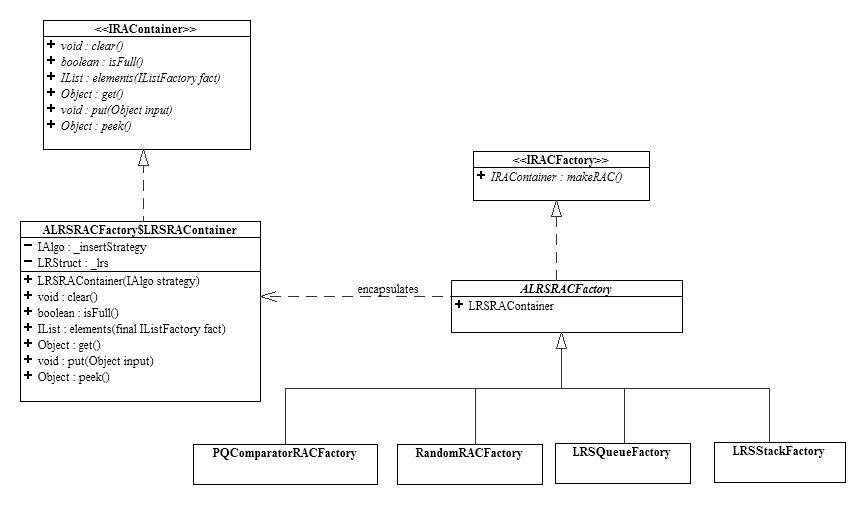
This is very similar to the RAC
presented in class except for one very
important difference: the IRAContainer.isEmpty()
method is absent.
A RAC behaves differently when it
is empty or non-empty; for example, calling get() on an empty RAC results in an
exception, while a non-empty RAC will return an object.
Therefore,
it makes sense for a RAC (IRAContainer)
to be able to accept a two-case visitor.
a)
Write the signatures for the methods of a visitor to the above RAC and
the signature the method that should be added as a result to IRAContainer:
public interface
IRACVisitor {
}
public interface
IRAContainer {
// … other methods not shown…
}
b) Write the code for the method(s) of LRSRAContainer (ALRSFactory$LRSRAContainer in the above UML class diagram) that implements the abstract method(s) you added to IRAContainer in part a).
Tip: To access the outer LRSRAContainer object from within an anonymous inner class inside a LRSRAContainer, use the syntax LRSRAContainer.this.
NO CONDITIONALS ARE ALLOWED IN YOUR SOLUTION!
5. In the Hangman project we represented a word whose characters were either visible or invisible as a modified list:
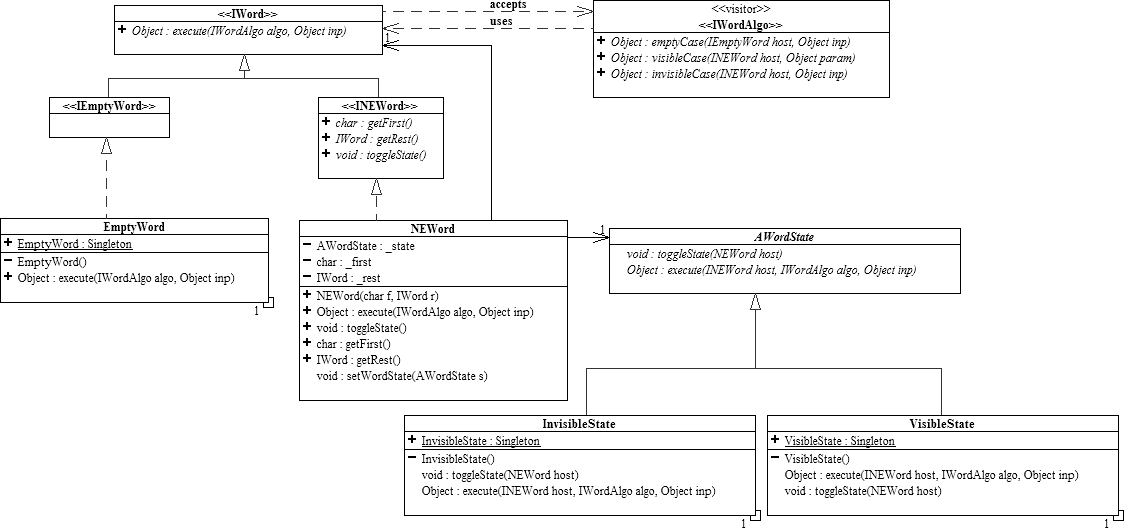
This model has several problems however:
· An NEWord in its invisible state does not actually represent an invisible word, but rather an invisible first. The rest of the NEWord could be either visible or invisible. Conversely, the same is true if the NEWord is in its visible state.
·
The state pattern used in NEWord tightly couples the visibility property to the composite
property of the word, even though those two properties really have nothing to do
with each other.
So, what we would like to do is to replace IWord
with IList, our immutable list
framework (see UML diagram below). Thus,
a Hangman word would be represented as a IList
of WordChar
objects (that you will be asked to design).
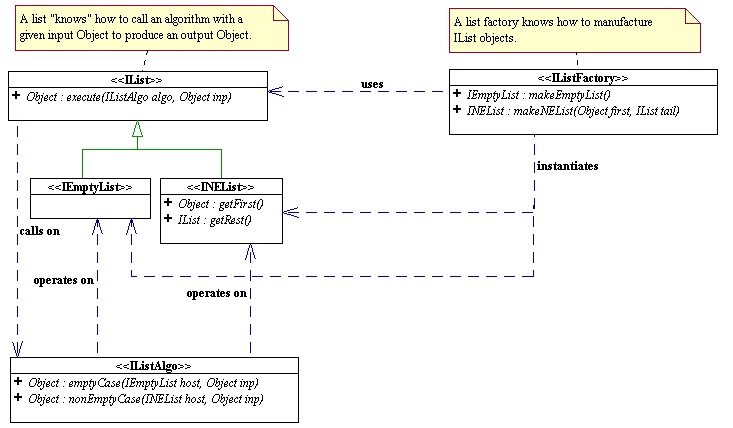
a) Design a class called WordChar
that represents a character in the hangman word. WordChar
is to be designed in such a way that the hangman word can simply be
represented as an IList of WordChar
objects. It is now the WordChar
that may be visible or invisible. Be sure to replicate all the non-list
functionality of the IWord
system including the ability to run
visibility-dependent algorithms, e.g. ToString,
IsVisible, GuessChar,
etc.
Draw the UML class diagram of your WordChar
model. Clearly
indicate the signatures (i.e return type, parameters type) of all methods and
appropriate access specifiers of all fields and methods. You do
not need to write any code.
b) Write the ToString algorithm, which is an IListAlgo, for your new word model designed in part a) to return the String representation of the hangman word (list of WordChar). Recall that a hangman word displays the actual character when it is visible and an underscore ('_') when it is invisible.