Suppose we have a two-player game in which each player takes turn making his/her move. We assume that the game will always terminate in a draw, win, or loss. We can conceptualize the game as a tree consisting of all the possible "game board" configurations with the initial configuration as a root node. Each node in the game tree corresponds to a possible configuration of the game. A leaf node corresponds to an end game configuration: a win, loss, or draw.
For the sake of definiteness, assume the players are John and Mary. We can imagine when John is to make a move, he will move to a game node that is best for him. What's best for John is based on some numerical value that he associates with each of next possible moves. How are the value of each of the game node calculated? Here is one such possible computation.
For each of the leaf node, John can assign a value of 1 if he wins, 0 if he ties, and -1 if he loses. Conceptually, John defines a "pay-off" function P as follows:
P (leaf) =
Now, John assigns a value, V(x), to a game node x, as follows:
V (x) =
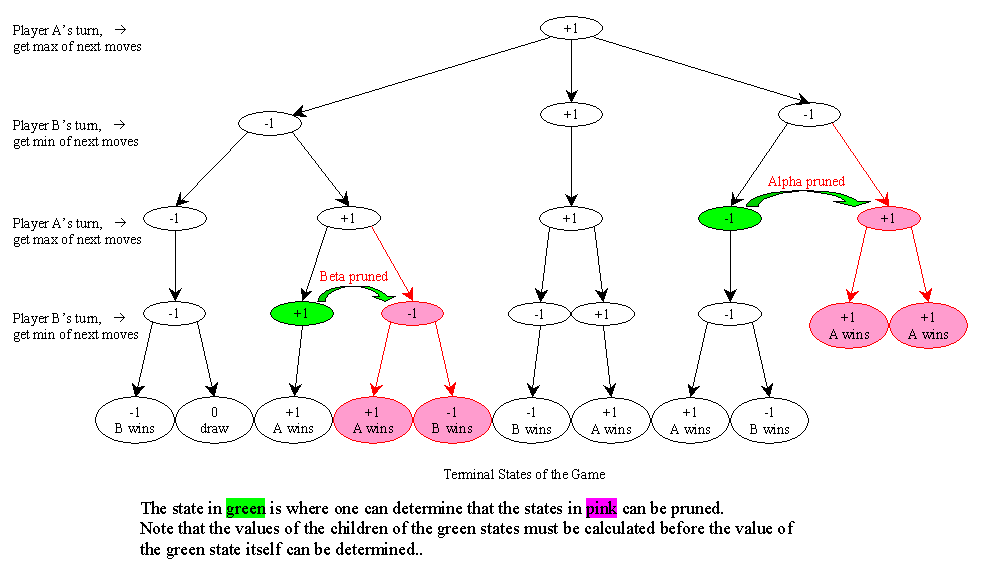
The heuristic here is that John would make a move to a node that has the maximum value for him, and Mary would do her best by going for the node that has the minimum value (from John's perspective). This game configuration computation is called the min-max strategy. Below is a fictitious game tree illustrating min-max and alpha-beta pruning. Alpha-beta pruning will be discussed in a latter section.

In general, it is not possible to get to all leaf nodes of a game. The best one can do is to examine the game tree up to certain depth. The min-max strategy with depth limitation can be expressed as follows.
Let P (n) be a pay-off function that a player uses to evaluate a game node n.
For a given player, the value of a node x at a depth d is:
V (x, d) =In computing the min/max value of a game tree node, we can skip ("prune") the evaluation of some of the children nodes using what is known as alpha-beta pruning.
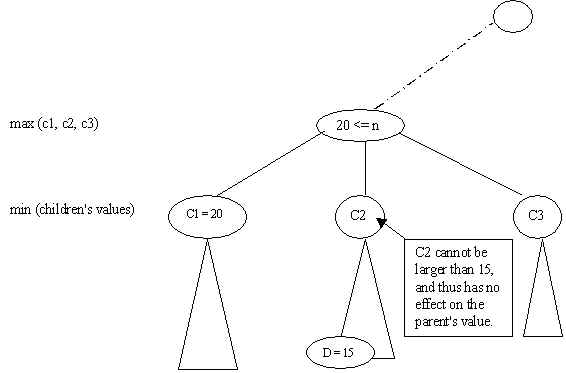
Let alpha be a lower bound for the value of a max node B, and let C be a child node of B. If the value v of a child of C is less or equal to alpha, then we can use v as a value for C and skip the rest of the children of C. This is called "alpha pruning". In the figure below, suppose we have (recursively) determined that the value of C1 is 20, then alpha = 20 is a lower bound for the parent (max) node. Now, suppose as we (recursively) compute the value for C2, we determine that the value of D, a child of C2, is 15. The best possible move for C2 cannot have a value larger than 15 and has no effect on the parent (max) node. Thus we can set the value of C2 to 15 and ignore the rest of the children of C2.
Let beta be an upper bound for the value of a min node B, and let C be a child node of B. If the value v of a child of C is greater or equal to beta, then we can use v as a value for C and skip the rest of the children of C. This is called "beta pruning". Exercise: draw a figure similar the one below to illustrate beta pruning.
Alpha-beta pruning can be expressed in terms of the min-max algorithm using a special kind of accumulator. We first describe an object-oriented formulation for the min-max algorithm.
A common approach to computing the max and min is to iterate over the available states. This involves casting the set of available states into some sort of linear ordering. But the statement of the min-max principle is not dependent on any linear ordering of the set. It simply prescribes a recursive application of V(s) onto the set. This is akin to the higher order function called “map”, familiar to functional programming practitioners. We thus express the min-max algorithm in terms of a map function rather than iteration. Since the actual map function is independent of the algorithm, it belongs as a service provided by the game board, and not as an integral part of the algorithm. The map method provided by the IBoardModel takes an abstract “lambda” object, IBoardLambda, and a generic input parameter. The map() method only depends on whether or not the board’s state is terminal, hence IBoardLambda has two corresponding methods: apply() for the non-terminal state and noApply() for the terminal states. The map method applies the lambda (with its input parameter) to all available valid move states from the current state. The lambda asks the board to make a move which also checks the status of the board, and recurs if necessary by asking the board to map it again. For efficiency reasons, it is best to accumulate the current extremum value and corresponding best move during the mapping. The responsibility to carry out this task is assigned to an abstract accumulator class, AAccumulator. It has an abstract updateBest() method that polymorphically performs the min or max determination both trivially and transparently, takes care of saving the maximum value (for this player) or the minimum value (for the other player) and its associated move and stores the result. It also has a factory method, makeOpposite(), to instantiate an accumulator for the other player.
The min-max algorithm can now be formulated as a class MinMax
that implements INextMoveStrategy.
Its method to compute the best next move is rephrased in the following OO
terms.
Ask the IBoardModel, board, to map the following recursive “helper” IBoardLambda, onto all valid moves from the current state with an appropriate initial AAccumulator, say acc.
1. Ask board to make the current move, passing it an IBoardStatusVisitor to do one of the following tasks associated with a possible resulting state.
· Player won: pass the current move and the value +1 to acc.updateBest().
· Player lost: pass the current move and the value -1 to acc.updateBest().
· Draw: pass the current move and the value 0 to acc.updateBest().
· Non-terminal state:
i. Ask board to map this helper algorithm onto the now available valid states with a new accumulator, nextAcc, for the other player.
ii. Pass the current move and the value obtained from nextAcc to acc.updateBest().
2.
Ask board to undo the
current move.
When the algorithm is finished, the initial accumulator, acc, will hold the best next move with its corresponding value.
The min-max algorithm formulated as shown does not rely on any concrete implementation of IBoardModel. Thus it can be used with any concrete type of games, as advertised in earlier discussions. It involves no external iterative loops, and closely approximates the abstraction of the min-max principle, making the code easier to write, more robust, more likely to be correct, and more flexible than traditional implementations. The Java code for the above OO formulation is almost a word-for-word translation.
Here are UML diagrams and javadoc for MinMax and the union of accumulators.
Last Revised 04/13/2005