Rice University - Comp 212 - Intermediate Programming

Spring 2006

• A running program consumes resources such as time (seconds) and space (bits).  Frequently, we abstract our units, and measure steps and objects, instead of seconds and bits.
• When comparing programs (or algorithms), you should first pay attention to gross differences in time or space consumed, for example, n^3 versus n^2 steps, rather than 3n versus 2n steps.
• For a few programs, the cost is fixed and can be calculated by examining the program text.  More frequently, however, cost depends on characteristics of the input, such as length.

• When we make gross comparisons of programs, we often refer to the ``order-of-magnitude'' of the cost.  The notation used is sometimes called ``Big-Oh,'' and is always of the form O(f(n)) where f(n) is some function over the positive integers.
• The Big-Oh notation simply means that the cost function is bounded by (is less than) some multiple of the function f(n).  For example, if we say
P = n^3 + O(n^2)
we mean that P equals n^3, plus some terms that are ``on the order of n^2''---i.e., they don't grow faster than kn^2, where k is some constant term.

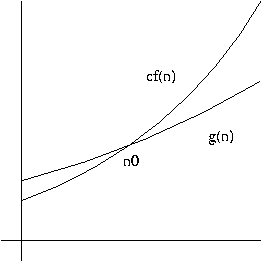
• More precisely,


Definition. A function g(n) is said to be O(f(n)), written

g(n) = O(f(n))
if there are positive integers c and n0 such that
0 <= g(n) <= cf(n)
for all n >= n0.
 
• In other words, O(f(n)) is the set of all functions h(n) such that there exist positive integers c and n0 such that
0 <= h(n) <= cf(n)
for all n >= n0.

• For example,


1+2+3+ ... +n = n(n+1)/2 = n^2/2 + n/2

1+2+3+ ... +n = n^2/2 + O(n)

1+2+3+ ... +n = O(n^2)

• Here are some equivalences that allow you to manipulate equations involving order-of-magnitude quantities:
• f(n) = O(f(n))
• K * O(f(n)) = O(f(n))
• O(f(n)) + O(f(n)) = O(f(n))
• O(f(n)) * O(g(n)) = O(f(n) * g(n))

• Also, the base to which a logarithm is computed doesn't affect the order of magnitude, because changing the base of the logarithm from 2 to c changes the value by a constant factor of log2(c).