In programming, it is often necessary to have objects with which one can store data, retrieve data when needed, and remove data when no longer needed. Such objects are instances of what we call container structures.
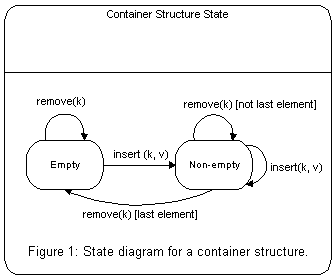
A mutable container structure is a system that may change its state from empty to non-empty, and vice-versa. For example, an empty container changes its state to non-empty after insertion of an object; and when the last element of a container is removed, its changes its state to empty. Figure 1 below diagrams the state transition of a container structure.

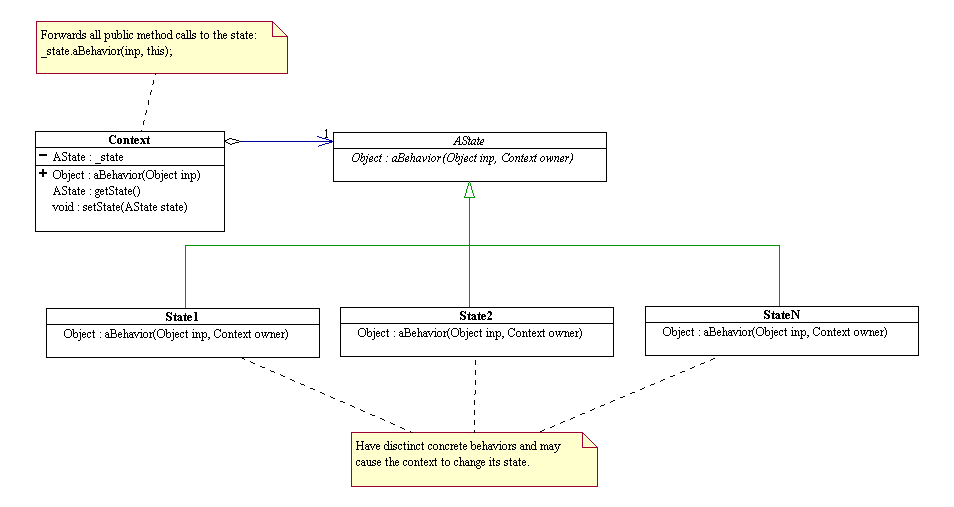
For each distinct state, the algorithms to implement the methods differ. For example, the algorithm for the retrieve method is trivial in the empty state -it simply returns null- while it is more complicated in the non-empty state. The system thus behaves as if it changes classes dynamically. This phenomenon is called “dynamic reclassification.” The state pattern is a design solution for languages that do not directly support dynamic reclassification. This pattern can be summarized as follow.
· Define an abstract class for the states of the system. This abstract state class should provide all the abstract methods for all the concrete subclasses.
· Define a concrete subclass of the above abstract class for each state of the system. Each concrete state must implement its own concrete methods.
· Represent the system by a class, called the context, containing an instance of a concrete state. This instance represents the current state of the system.
· Define methods for the system to return the current state and to change state.
· Delegate all requests made to the system to the current state instance. Since this instance can change dynamically, the system will behave as if it can change its class dynamically.
Below is the UML class diagram for the state design pattern.
A mutable linear recursive structure (LRStruct) can be in the empty state or in a non-empty state. If it is empty, it contains no object. Otherwise, it contains an object called first, and a LRStruct object called rest. When we insert a data object into an empty LRStruct, it changes it state to non-empty. When we remove the last element from an non-empty LRStruct, it changes its state to empty. We model a LRStruct using the state pattern, and as in the case of the immutable list, we also apply the visitor pattern to obtain a framework. Below is the UML class diagram of the LRStruct framework. Because of the current limitation of our tool, we are using the Object[] input notation to represent the variable argument list Object... input. Click on the diagram to see the full documentation. Click here to see the code. We will study the implementation code in the next lecture.
The public constructor:
LRStruct()
and the methods:
insertFront(...)
removeFront(...)
getFirst()
setFirst(...)
getRest()
setRest(...),
of LRStruct expose the structure of an LRStruct to the client and constitute the intrinsic structural behavior of an LRStruct. They form a minimal and complete set of methods for manipulating an LRStruct. Using them, a client can create an empty LRStruct, store data in it, and remove/retrieve data from it at will.
The method,
Object execute(IAlgo algo, Object... inp),
is called the extensibility
"hook". It allows the client to add an open-ended number of
new application-dependent behaviors to the data structure LRStruct,
such as computing its length or merging one LRStruct
with another, without modifying any of the existing code. The
application-dependent behaviors of LRStruct
are extrinsic behaviors and are encapsulated in a union represented
by a visitor interface called IAlgo.
When a client programs with LRStruct, he/she only sees the public methods of LRStruct and IAlgo . To add a new operation on an LRStruct , the client writes appropriate concrete classes that implements IAlgo . For example,
public class DoSomethingWithLRS implements IAlgo {
/* concrete code goes here...*/
}
The framework dictates the overall design of an algorithm on LRStruct : since an algorithm on LRStruct must implement IAlgo , there must be some concrete code for emptyCase(...) and some concrete code for nonEmptyCase(...). For example,
public class DoSomethingWithLRS implements IAlgo {
// fields and constructor code...
public Object emptyCase(LRStruct host, Object... inp) {
// some concrete code here...
return some Object; // may be null.
}
public Object nonEmptyCase(LRStruct host, Object... inp) {
// some concrete code here...
return some Object; // may be null.
}
}As illustrated in the above, an algorithm on LRStruct is "declarative" in nature. It does not involve any conditional to find out what state the LRStruct is in in order to perform the appropriate task. It simply "declares" what needs to be done for each state of the host LRStruct , and leaves it to the polymorphism machinery to make the correct call. Polymorphism is exploited to minimize flow control and reduce code complexity.
To perform an algorithm on an LRStruct , the client must "ask" the LRStruct to "execute" the algorithm and passes to it all the inputs required by the algorithm.
LRStruct myList = new LRStruct(); // an empty list
// code to call on the structural methods of myList, e.g. myList.insertFront(/*whatever*/)
// Now call on myList to perform DoSomethingWithLRS:
Object result = myList.execute(new DoSomethingWithLRS(/* constructor argument list */), -2.75, "abc");
Without knowing how LRStruct is implemented, let us look an example of an algorithm on an LRStruct .
Consider the problem of inserting an Integer object in order into a sorted list of Integers. Let us contrast the insert in order algorithms between IList, the immutable list, and LRStruct, the mutable list.
import listFW.*;
public class InsertInOrder implements IListAlgo {
private IListFactory _fact;
public InsertInOrder(IListFactory lf) {
_fact = lf;
}
/**
* Simply makes a new non-empty list with the given
* parameter n as first.
* @param host an empty IList.
* @param n n[0] is an Integer to be inserted in order into host.
* @return INEList.
*/
public Object emptyCase(IEmptyList host, Object... n) {
return _fact.makeNEList(n[0], host);
}
/**
* Based on the comparison between first and n,
* creates a new list or recur!
* @param host a non-empty IList.
* @param n an Integer to be inserted in order into host.
* @return INEList
*/
public Object nonEmptyCase(INEList host, Object... n) {
return (Integer)n[0] < (Integer)host.getFirst() ?
_fact.makeNEList(n[0], host):
_fact.makeNEList(host.getFirst(),
(IList)host.getRest().execute(this, n[0]));
}
}
|
import lrs.*;
public class InsertInOrderLRS implements IAlgo {
public static final InsertInOrderLRS Singleton
= new InsertInOrderLRS();
private InsertInOrderLRS() {
}
/**
* Simply inserts the given parameter n at the front.
* @param host an empty LRStruct.
* @param n n[0] isan Integer to be inserted in order into host.
* @return LRStruct
*/
public Object emptyCase(LRStruct host, Object... n) {
return host.insertFront(n[0]);
}
/**
* Based on the comparison between first and n,
* inserts at the front or recurs!
* @param host a non-empty LRStruct.
* @param n n[0] is an Integer to be inserted in order into host.
* @return LRStruct
*/
public Object nonEmptyCase(LRStruct host, Object... n) {
if ((Integer)n[0] < (Integer)host.getFirst()) {
return host.insertFront(n[0]);
}
else {
return host.getRest().execute(this, n[0]);
}
}
}
|
||
| Note that the insert in order algorithm for LRStruct need not create any new list and thus needs no factory. | |||