Rice University - Comp 212 - Intermediate Programming

Spring 2008

Lecture #37: Heaps and Heap Sort; Merge Sort, Quick Sort

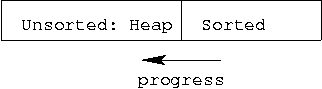
Heap Sort

Heap Sort, like Selection Sort, is a hard-split, easy-join method.
Think of Heap Sort as an improved (faster) version of Selection Sort.

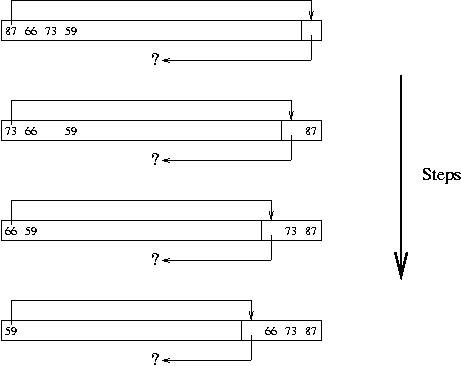
Specifically, split(), which finds the largest element in the subarray, is made to run in O(log n) steps instead of O(n) steps, where n is the subarray length.
Since split() is performed n times, where n is the (overall) array length, Heap Sort takes O(n log n) steps.

How is split() sped up?

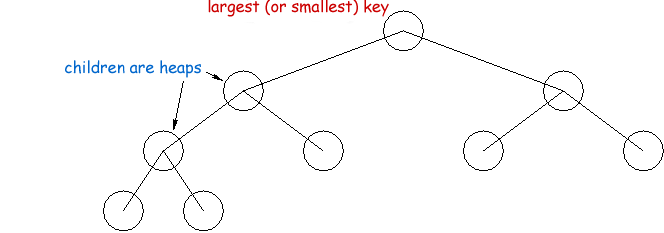
The elements in the unsorted portion of the array are organized into a heap. A heap is a data structure that is optimized for repeatedly finding and removing the largest (or smallest) element.

What is a Heap?

A "complete" tree is a minimum height tree with all the nodes on the lowest level in their left-most positions. That is, the tree is completely filled from the top with any extra elements strictly on one side (left) of the lowest level. Note that in a complete tree, ther is at most a variation of 1 in path lengths from the root to the leaves.
A heap is a binary tree that
1. is complete and
2. also exhibits the heap property:
  - the root, if non-null, is the largest (or smallest) key in the tree, and
  - its left and right subtrees are themselves heaps.

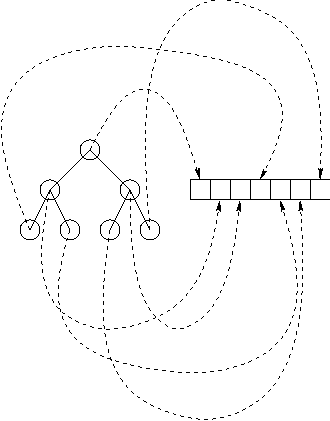
Implementing a Heap?

Heap Sort Basics

Heap Sort: split()

public int split(int[] A, int lo, int hi) {
    // Swap A[hi] and A[lo].
    int temp = A[hi];
    A[hi] = A[lo];
    A[lo] = temp;

    // Restore the heap property by ``sifting down''
    // the element at A[lo].
    Heapifier.Singleton.siftDown(A, lo, lo, hi - 1);

return hi;
}

Example of siftDown()

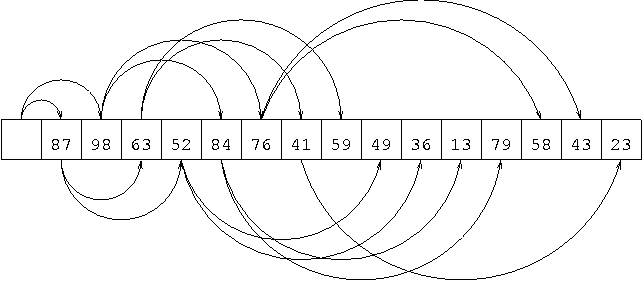
siftDown(): The Implementation

public void siftDown(int[] A, int lo, int cur, int hi) {
    int dat = A[cur];             // hold on to data.
    int child = 2 * cur + 1 - lo; // index of left child of A[cur].
    boolean done = hi < child;

while (!done) {

        if (child < hi && A[child + 1] > A[child]) {
            child++;
        } // child is the index of the larger of the two children.

        if (A[child] > dat) {
            A[cur] = A[child];
            cur = child;
            child = 2 * cur + 1 - lo;
            done = hi < child;
        }                     // A[cur] is greater than its children.
        else {                // A[cur] >= A[child].
            done = true;      // heap condition is satisfied.
        }                     // A[cur] is greater than its children.
    }                         // location found for dat.
    A[cur] = dat;
}

Initializing the Heap: HeapSorter()

public class HeapSorter extends ASorter {
    public HeapSorter(int[] A, int lo, int hi) {
        for (int cur = (hi - lo + 1) / 2; cur >= lo; cur--) {
            Heapifier.Singleton.siftDown(A, lo, cur, hi);
        }
    }
// etc. . . }

Merge Sort and Quick Sort

Link to Merge Sort and Quick Sort Notes

Link to Merge Sort Code

Link to Quick Sort Code

Summary of Sorting

	Best-case Cost	Worst-case Cost
Selection	O(n²)	O(n²)
Insertion	O(n)	O(n²)
Heap	O(n log n)	O(n log n)
Merge	O(n log n)	O(n log n)
Quick	O(n log n)	O(n²)

Selection sort performs the least swaps, O(n), in the worst case.
Insertion sort is best if the array is nearly or already sorted.
Heap sort performs a constant factor more comparisons than Merge sort
Merge sort requires extra storage proportional in size to the input.
Quick sort typically (expected case) outperforms Heap and Merge sort because of its simplicity.

By Alan Cox and Dung "Zung" Nguyen

Last Revised 03/31/2008 09:32 AM