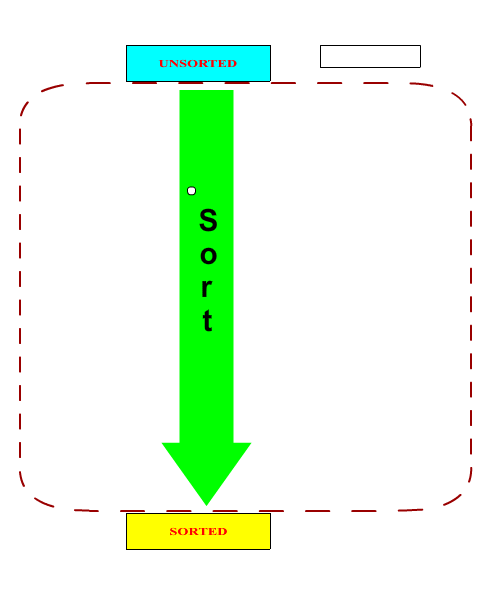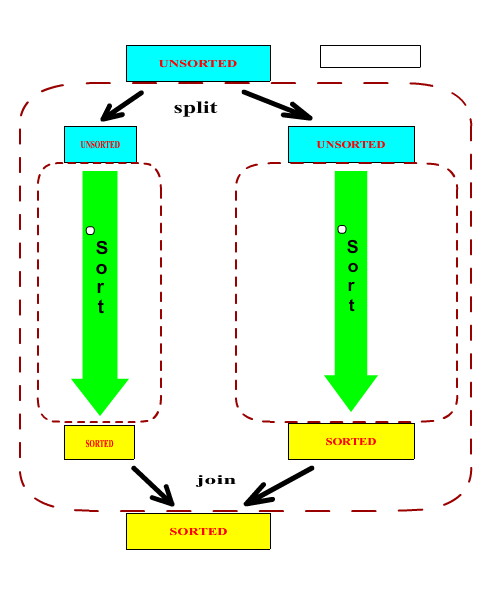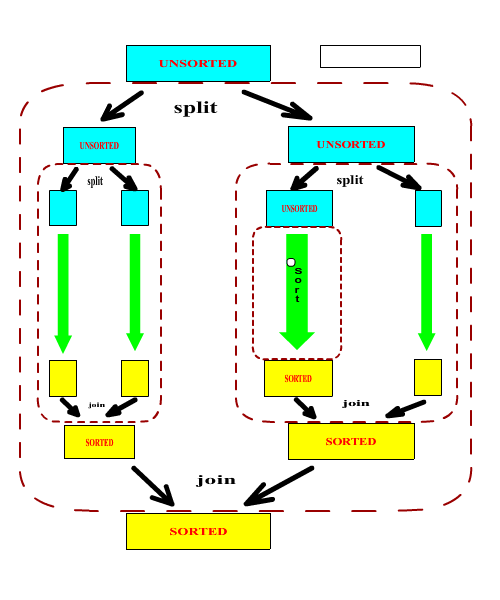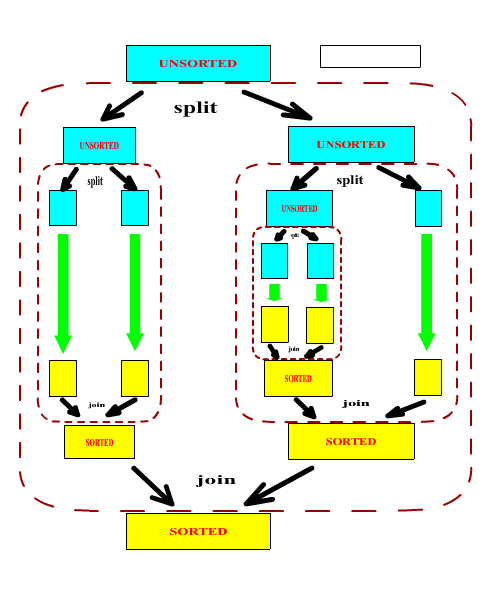
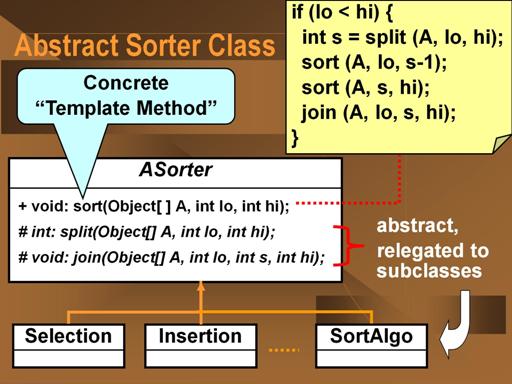
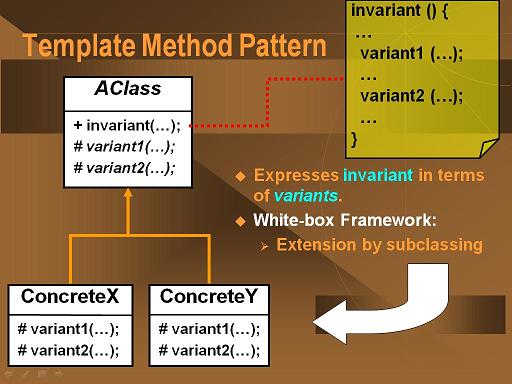
In order to create a sorter that can actually perform a sorting operation, we need to subclass the above ASorter class and implement the abstract split and join methods. It should be noted that in general, the split and join methods form a matched pair. One can argue that it is possible to write a universal join methods (a merge operation) but it would be highly inefficent in most cases.
Example 1: Selection Sort
Tradionally, an in-place selection sort is performed by selecting the smallest (or largest) value in the array and placing it in the right-most location by either swapping it with the right-most element or by shifting all the in-between elements to the left. The selection and swapping/shifting process then repeated with the sub-array to the left of the newly placed element. This continues until only one element remains in the array. A selection sort is commonly used to do something like a sort group of people into ascending height.
Below is an animation of a traditional selection sort algorithm:
| Traditional Selection Sort Algorithm |
|---|
|
In terms of the Merritt sorting paradigm, a selection sort can be broken down into a splitting process that is the same as the above selection process and a trivial join process. Looking at the above selection and swap/shift process, we see that it is describing a the splitting off of a single element, the smallest, from an array. The process repeats recursively until there is nothing more to split off. The sorting of a single element is a no-op, so after that the recursion rolls back out though the joining process. But the joining process is trivial, a no-op, because the elements are already in their corret positions. The beauty of Merritt's insight is the realize that by considering a no-op as an operational part of a process, all the different types of binary comparison-based sorting could be unified under a common framework.
Below is an animation of a Merritt selection sort algorithm:
| Merritt Selection Sort Process |
|---|
|
The code to implement a selection sorter is straightforward. One need only implement the split and join methods where the split method always returns the lo+1 index because the smallest value in the (sub-)array has been moved to the index lo position. Because the bulk of the work is being done in the splitting method, selection sort is classified as an "hard split, easy join" sorting process.
In the Java implementation of the SelectionSorter class below, the split method splits off the extrema (minimum, here) value from the sub-array, while the join method is a no-op.
SelectionSorter class
package sorter;
/**
* A concrete sorter that uses the Selection Sort technique.
*/
public class SelectionSorter extends ASorter
{
/**
* The constructor for this class.
* @param iCompareOp The comparison strategy to use in the sorting.
*/
public SelectionSorter(AOrder iCompareOp)
{
super(iCompareOp);
}
/**
* Splits A[lo:hi] into A[lo:s-1] and A[s:hi] where s is the returned value of this function.
* This method places the "smallest" value in the lo position and splits it off.
* @param A the array A[lo:hi] to be sorted.
* @param lo the low index of A.
* @param hi the high index of A.
* @return lo+1 always
*/
protected int split(Object[] A, int lo, int hi)
{
int s = lo;
int i = lo + 1;
// Invariant: A[s] <= A[lo:i-1].
// Scan A to find minimum:
while (i <= hi)
{
if (aOrder.lt(A[i], A[s]))
s = i;
i++; // Invariant is maintained.
} // On loop exit: i = hi + 1; also invariant still holds;
// this makes A[s] the minimum of A[lo:hi].
// Swapping A[lo] with A[s]:
Object temp = A[lo];
A[lo] = A[s];
A[s] = temp;
return lo + 1;
}
/**
* Joins sorted A[lo:s-1] and sorted A[s:hi] into A[lo:hi].
* This method does nothing. The sub-arrays are already in proper order.
* @param A A[lo:s-1] and A[s:hi] are sorted.
* @param lo the low index of A.
* @param s
* @param hi the high index of A.
*/
protected void join(Object[] A, int lo, int s, int hi)
{
}
}
What's interesting to note here is what is missing from the above code. A tradional selection sort aalgorithm is implemented using a nested double loop, one to find the smallest value and one to repeatedly process the ever-shrinking unsorted sub-array. Notice that the above code only has a single loop, which coresponds to the inner loop of a traditional implementation. The outer loop is embodied in the recursive nature of the sort template method in the ASorter superclass.
Notice also that the selection sorter implementation does not include any explicit connection between the split and join operations nor does it contain the actual sort method. These are all contained in the concrete sort method of the superclass. We describe the SelectionSorter class as a component in a framework (technically a "white box" framework, as described above). Frameworks display inverted control where the components provide services to the framework. The framework itself runs the algorithms, here the high level, templated sorting process, and call upon the services provided by the components to fill in the necessary processing pieces, e.g. the split and join procedures.
Example 2: Insertion Sort
Tradionally, an in-place insertion sort is performed by starting from one end of the arry, say the left end, and performing an in-order insertion of an element into the sub-array to its left. The next element to the right is then chosen and the insertion process repeated. At each insertion, the sorted sub-array on the left grows until encompasses the entire array. An insertion sort is a very typical way in which people will order a set of playing cards in their hand.
Below is an animation of a traditional insertion sort algorithm:
| Traditional Insertion Sort Algorithm |
|---|
|
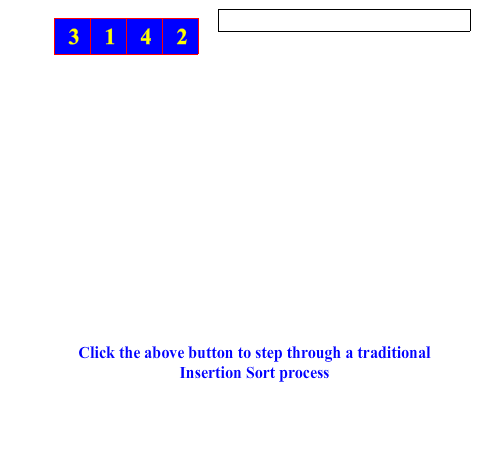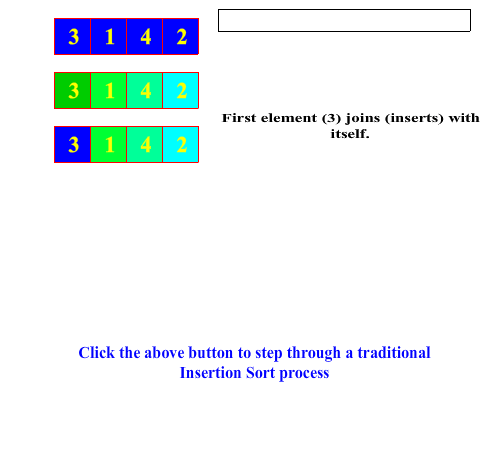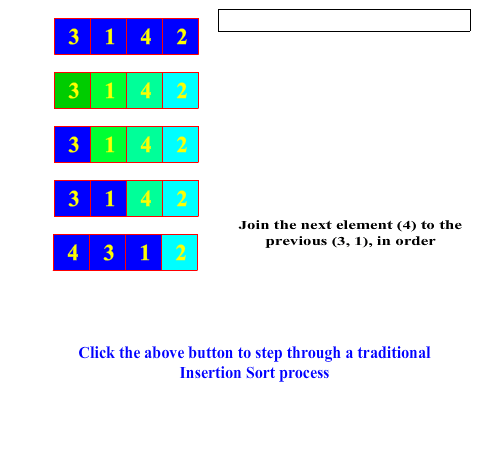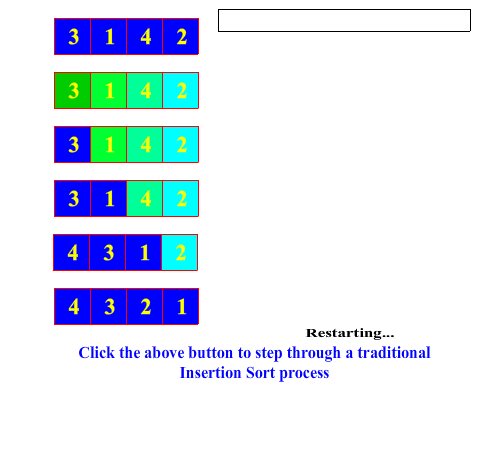
In the Merrit paradigm, the insertion sort first splits the array or sub-array into two pieces simply by separating the right-most element. Recursively, the splitting process proceeds to from the right to the left until a single element is left in the sub-array. Sorting a one element array is a no-op, so then the recursion unwinds with the join process. The join process combines each single split-off element with its sorted sub-array partner to its left by performing an in-order insertion. This proceeds as the recusion unwinds until the entire array is fully sorted. In contrast to the selection sort, the bulk of the work is being done in the join method, hence classifying insertion sort as an "easy split, hard join" sorting process.
Below is an animation of a Merritt insertion sort algorithm:
| Merritt Insertion Sort Process |
|---|
|
In the Java implementation of the selection sorter below, the split method simply splits off the right-most element of the sub-array. The join method performs an in-order insertion of the single split-off element into the larger sub-array to its left.
InsertionSorter class
package sorter;
/**
* A concrete sorter that uses the Insertion Sort technique.
*/
public class InsertionSorter extends ASorter
{
/**
* The constructor for this class.
* @param iCompareOp The comparison strategy to use in the sorting.
*/
public InsertionSorter(AOrder iCompareOp)
{
super(iCompareOp);
}
/**
* Splits A[lo:hi] into A[lo:s-1] and A[s:hi] where s is the returned value of this function.
* This simply splits off the element at index hi.
* @param A the array A[lo:hi] to be sorted.
* @param lo the low index of A.
* @param hi the high index of A.
* @return hi always.
*/
protected int split(Object[] A, int lo, int hi)
{
return (hi);
}
/**
* Joins sorted A[lo:s-1] and sorted A[s:hi] into A[lo:hi]. (s = hi)
* The method performs an in-order insertion of A[hi] into the A[lo, hi-1]
* @param A A[lo:s-1] and A[s:hi] are sorted.
* @param lo the low index of A.
* @param s
* @param hi the high index of A.
*/
protected void join(Object[] A, int lo, int s, int hi)
{
int j = hi; // remember s == hi.
Object key = A[hi];
// Invariant: A[lo:j-1] and A[j+1:hi] are sorted and key < all elements of A[j+1:hi].
// Shifts elements of A[lo:j-1] that are greater than key to the "right" to make room
// for key.
while (lo < j && aOrder.lt(key, A[j-1]))
{
A[j] = A[j-1];
A[j-1] = key;
j = j - 1; // invariant is maintained.
} // On loop exit: j = lo or A[j-1] <= key. Also invariant is still true.
// A[j] = key;
}
}
Exercise 1
The authors were once challenged that the Merritt template-based sorting paradigm could not be used to describe the Shaker Sort process (a bidirectional Bubble or Selection sort). See for instance, http://en.wikipedia.org/wiki/Cocktail_sort. However, it can be done is a very straightforward manner. There are a number of viable solutions. Hint: think about the State Design Pattern. (The solution is left to the student but is available from the authors if proof of non-student status is provided.)
For more examples, please see download the demo code. Please note that the ShakerSort code is disabled due to its use as a student exercise.