Summary: The derivation of the kinetics of a perfectly elastic the collision of two spherical objects of different mass
Consider the perfectly elastic collision between two massive point objects moving with individual velocities:
| General Two-Body Collision |
|---|
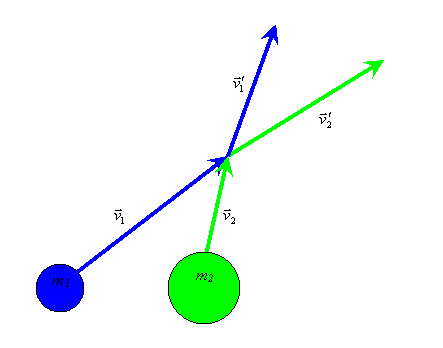 |
The problem is much more easily solved in the center of mass coordinate system because the total momentum in that coordinate system is zero. We can find the motion of the center of mass by utilizing the definition that the net momentum is equal to the total mass times the velocity of the center of mass:
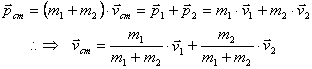
We can thus do the transformation to the center-of-mass coordinate system:

Note that the total momentum in the center-of-mass frame is indeed zero. The mass factor in the momentum equations is called the “reduced mass”.
In this coordinate system, we have the following picture:
| General Two-Body Collision in the Center-of-Mass frame |
|---|
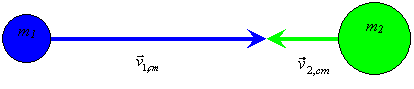 |
The solution to the elastic recoil problem is trivial now. Each mass simply rebounds with the negative of its original velocity. There are a number of ways to prove this, all of which come down to the same statement: To conserve both momentum and energy, the only solutions when the total initial momentum is zero are that the final momenta (or velocities) are the original momenta (or velocities) which is the non-interacting case or that the final momenta (or velocities) are the negatives of the original momenta (or velocities). This assumes, of course, that mass is conserved on a particle by particle basis.
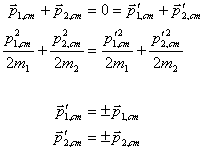
It is nice to talk about the “impulse” of the collision, which is the change in momentum due to the collision:
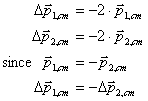
The last equation is simply a statement of Newton’s Third Law of Motion.(“For every action there is an equal an opposite reaction”).
Since the impulse is a change in momentum, it is invariant under the Galilean transformation back to the laboratory (non-center-of-mass) coordinates.
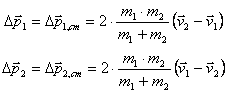
The change in velocity is thus
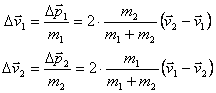
To check this answer, consider the case where the masses are equal:
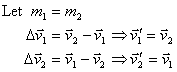
Another interesting limit is if one mass is much, much greater than the other, say here, mass #2 is much, much greater than mass #1. In this limit, the change in velocity for ball #1 is 2 times time difference between their original velocities, i.e. it simply elastically bounces off the other ball. Ball #2 on the other hand, has a change of velocity that tends towards zero, that is, it is unaffected by the much smaller ball bouncing off of it.