COMP 310
|
Lec21: Extended Visitors Example - Self-balancing Trees |
|
|
Binary Search Trees (BST's) are great for storing data and give us great speed...or do they?
One really wants BSTs and other trees to be balanced for optimal performance!
Kind of like an n-ary tree but with multiple pieces of data on each tree root (node).
An extension of the idea of a BST where the ordering of the data in the child trees depends on the data in the parent node.
The main points of this discussion, besides teaching you about 2-3-4 and B-trees, is for you to see the following in action:
A running program consumes resources such as time (seconds) and space (bits). Frequently, we abstract our units, and measure steps and objects, instead of seconds and bits.
When comparing programs (or algorithms), you should first pay attention to gross differences in time or space consumed, for example, n3 versus n2 steps, rather than 3n versus 2n steps.
For a few programs, the cost is fixed and can be calculated by examining the program text. More frequently, however, cost depends on characteristics of the input, such as length.
When we make gross comparisons of programs, we often refer to the ``order-of-magnitude'' of the cost. The notation used is sometimes called ``Big-Oh,'' and is always of the form O(f(n)) where f(n) is some function over the positive integers.
The Big-Oh notation simply means that the cost function is bounded by (is less than) some multiple of the function f(n). For example, if we say
P = n3 + O(n2)
we mean that P equals n3, plus some terms that are ``on the order of n2''---i.e., they don't grow faster than kn2, where k is some constant term.
More precisely,
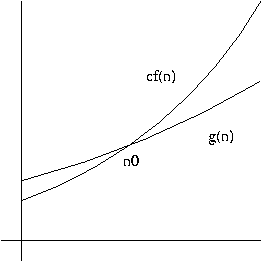
Definition. A function g(n) is said to be O(f(n)), written
g(n) = O(f(n))
if there are positive integers c and n0 such that
0 <= g(n) <= cf(n)
for all n >= n0.
In other words, O(f(n)) is the set of all functions h(n) such that there exist positive integers c and n0 such that
0 <= h(n) <= cf(n)
for all n >= n0.
For example,
1+2+3+ ... +n = n(n+1)/2 = n2/2 + n/2
1+2+3+ ... +n = n2/2 + O(n)
1+2+3+ ... +n = O(n2)
Here are some equivalences that allow you to manipulate equations involving order-of-magnitude quantities:
Also, the base to which a logarithm is computed doesn't affect the order of magnitude, because changing the base of the logarithm from 2 to c changes the value by a constant factor of log2(c).
(written by Alan Cox)
Big-Oh tells us how a cost of running a program (algorithm) scales with respect to n for large values of n, e.g. linearly, quadraticly, logarithmically, etc. The slower the cost rises with n, the better, so long as we are dealing with large values of n.
© 2012 by Stephen Wong