COMP 310
|
Lec09: MVC and Collision Handling |
|
|
Download the JAR file and run it (will not run as an applet because it accesses the local file system to store configurations).
Download and unzip some saved ecosystems and species that can be loaded into BuggerLab.
The MVC pattern enables us to decouple the view (the user interface portion) from the model (the back-end computations) in a large system. This decoupling will allow
The view and/or model to be changed without affecting the other.
Multiple views to be used, possibly simultaneously, with a single model.
Multiple model components to be seamlessly integrated behind the view.
The model and the view do not know anything about each other. Their communications consist of calling methods on interfaces to the rest of the system. The model and view must provide public methods (services) that can be used to communicate to them. Note that these services need not be standardized or abstracted, while the services they desire from the rest of the system must be abstracted into interfaces. (Why?)
The model and the view are connected by adapters that translate the interfaces into the provided services.
The controller is the only part of the system that knows the concrete classes being used by the view and by the model. The controller's job is to:
Instantiate the model and the view.
Instantiate and install the adapters that implement the interfaces that the model and view need to communicate. The adapters will translate the calls to their interface implementations into calls onto the provided services of the model or view.
The adapters installed into the model will translate/adapt calls from the model to the view.
The adapters installed into the view will translate/adapt the calls from the view to the model.
The controller will initiate any necessary start-up procedure.
If the model or view is changed, then the controller will usually need to be changed as well, but any effect should be contained to only the controller.
The controller should be fairly simple and should never contain any "business logic". If it becomes overly complicated, this is a sign that it is doing work that belongs in either the view or more likely, the model. Is the model missing a module or a layer?
Criteria for determining if methods belong on the same or different adapter interfaces:
Methods that are concerned with different aspects of the same general operation belong on the same adapter interface.
Methods that are completely decoupled from other methods belong on separate adapter interfaces.
For instance, the methods used to start a new game should be separate from those used to control the game while it is running.
MVC Design for BallWar (Illustrative purposes only--Individual student's designs are not required to look exactly like this!):
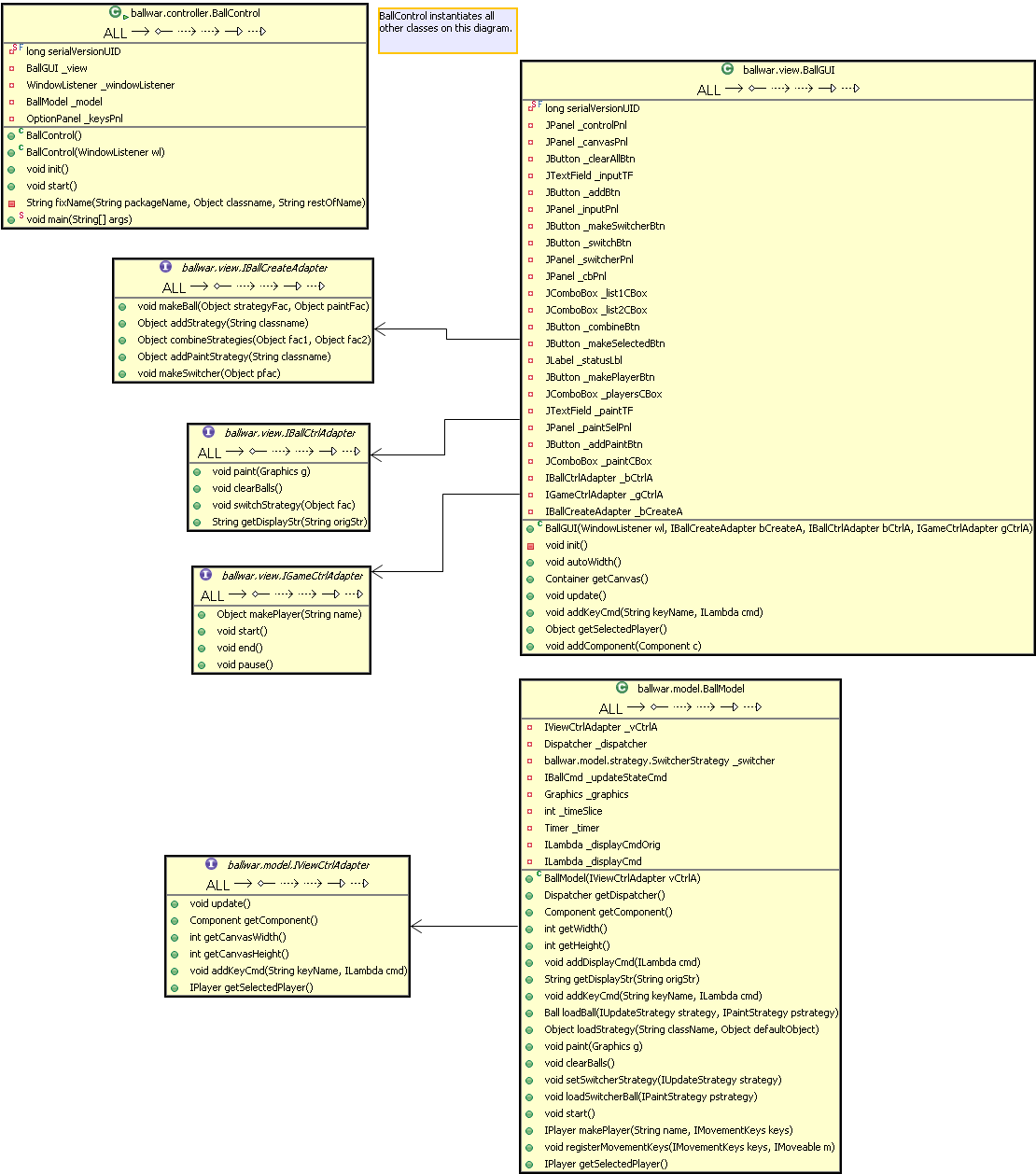
See the beginning of the discussion in Lec08.
Elastic collisions based on mass of the ball:
Basic physics: 2-Body Elastic Collisions
Make sure that the other ball does not have infinite mass (mass = Double.POSITIVE_INFINITY)! (Note: balls with infinite mass and non-zero velocities technically have infinite kinetic energy, so they tend to continuously add energy to the system, which quickly causes problems.)
AElasticMassCollisionCmd: An abstract IBallCmd superclass that provides protected utility methods that subclasses can use to calculate the effects of an elastic collision that depends on the mass of the balls. Read the documentation in the class carefully!
Basic recipe for a collision command:
Make sure that the other ball is not yourself! Remember that the dispatcher sends the command to everybody!
Are the two balls within collision distance?
If so, then proceed to calculate the effect of the collision on each other.
Calculate the reduced mass of the two-ball system
Use the reduced mass and other parameters to calculate the impulse of the collision. The position of the source ball will be "nudged" out of collision distance during this calculation.
Update the velocities of each ball and call its post-collision update behavior (a method on its update strategy). Note that the same method can be used to update either the source or target balls simply by switching the parameters and negating the impulse.
Otherwise, the command should end. The dispatcher will send the command to the next ball to be processed.
Nudging:
Because of the discrete nature of the movement of the balls and because the Ballworld system uses a single-pass updating mechanism (vs. a two-pass system where updating behaviors are calculated on the first pass and executed on a second pass), the balls may not be in the exact positions that one would expect them to be when they contact each other.
It is non-trivial to calculate the exact theoretical contact position of the two balls, so the AElasticMassCollisionCmd class pretends that the radius of the balls is exactly the sise such that the initial contact between the balls occurrs right at their current location.
In such, all calculations are based off of the "normal vector" which runs from the center of the source ball, through the point of contact between the balls, to the center of the target ball. This is the line that is normal to the plane of contact between the two balls, if their radii where exactly the size such they just touched at their current locations. A round or spherical surface can only exert a force along the normal to its tangential planes.
Theoretically, this normal line would be co-linear with the difference in velocities between the two balls (their relative motion, which is used to calculate the impulse), but in actuality, the two are not co-linear.
The shortest distance to move the source ball to get it out of collision distance with the target ball is along the normal direction. A "nudge" factor is introduced to insure that that the source ball is far enough away to not "double collide" with the target ball. (Why don't you move the target ball?)
© 2010 by Stephen Wong