COMP 310 Spring 2010	Lec16:  The Extended Visitor Design Pattern

A now, for something completely different...(well, maybe not that different...)

Balanced Trees

Binary Search Trees (BST's) are great for storing data and give us great speed...or do they?

1. Trees offer much faster access than lists, but only if the tree so long as all the branches are nearly the same length, i.e. "balanced".
2. A balanced tree gives O(log n) behavior, while lists give O(n) behavior.  (See below.for a quick refresher on "Big-Oh" analysis of programs.)
3. Worst case scenario for an unbalanced tree is O(n) behavior.

One really wants BSTs and other trees to be balanced for optimal performance!

2-3-4 Trees / B-Trees

Kind of like an n-ary tree but with multiple pieces of data on each tree root (node).

An extension of the idea of a BST where the ordering of the data in the child trees depends on the data in the parent node.

• See the PowerPoint Presentation!   (web-based presentation  -- animations may not run)

• See the OOPSLA 2002 Poster! (>740KB PNG file!)

• Read the OOPSLA 2002 paper in PDF format!

• See the demo!

• Compare the above demo to a demo of the traditional algorithms.    Here is the one of the clearest explanations of the traditional insertion and deletion algorithms from Prof. Neli Zlatereva at Central Connecticut State Univ..

Extended Visitor Design Pattern

Regular Visitor Design Pattern:

• Has an invariant number of hosts that can accept (execute) a variant number of visitors.

• Has one method (case) on every visitor that corresponds with every host type.  Each host calls only its corresponding case method.

• To add another host is to change an invariant, hence lots of trouble.   Must change very visitor.

• Does not allow for default behavior on a per-visitor basis.

Extended Visitor Design Pattern:

• Has a single, parameterized method, "caseAt", on the visitor that every host uses.

• Each host has a unique identifier that is used as the ID pameter for the caseAt method.

• The number of host types is now variant as well.

• A default behavior can be defined that applies to all unknown hosts.   Can be defined on a per-visitor basis.

Please read the student-written presentation of the extended visitor pattern.

Super-Quickie Primer:

Accounting For The Resources Used By Computations:  "Big-Oh" notation

A running program consumes resources such as time (seconds) and space (bits).  Frequently, we abstract our units, and measure steps and objects, instead of seconds and bits.

When comparing programs (or algorithms), you should first pay attention to gross differences in time or space consumed, for example, n³ versus n² steps, rather than 3n versus 2n steps.

For a few programs, the cost is fixed and can be calculated by examining the program text.  More frequently, however, cost depends on characteristics of the input, such as length.

When we make gross comparisons of programs, we often refer to the ``order-of-magnitude'' of the cost.  The notation used is sometimes called ``Big-Oh,'' and is always of the form O(f(n)) where f(n) is some function over the positive integers.

The Big-Oh notation simply means that the cost function is bounded by (is less than) some multiple of the function f(n).  For example, if we say

P = n³ + O(n²)

we mean that P equals n³, plus some terms that are ``on the order of n²''---i.e., they don't grow faster than kn², where k is some constant term.

More precisely,

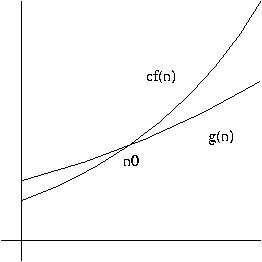
Definition. A function g(n) is said to be O(f(n)), written

g(n) = O(f(n))

if there are positive integers c and n0 such that

0 <= g(n) <= cf(n)

for all n >= n0.

In other words, O(f(n)) is the set of all functions h(n) such that there exist positive integers c and n0 such that

0 <= h(n) <= cf(n)

for all n >= n0.

For example,

1+2+3+ ... +n = n(n+1)/2 = n²/2 + n/2

1+2+3+ ... +n = n²/2 + O(n)

1+2+3+ ... +n = O(n²)

Here are some equivalences that allow you to manipulate equations involving order-of-magnitude quantities:

• f(n) = O(f(n))
• K * O(f(n)) = O(f(n))
• O(f(n)) + O(f(n)) = O(f(n))
• O(f(n)) * O(g(n)) = O(f(n) * g(n))

Also, the base to which a logarithm is computed doesn't affect the order of magnitude, because changing the base of the logarithm from 2 to c changes the value by a constant factor of log2(c).

(written by Alan Cox)

Quick and Dirty Explanation:

Big-Oh tells us how a cost of running a program (algorithm) scales with respect to n for large values of n, e.g. linearly, quadraticly, logarithmically, etc.   The slower the cost rises with n, the better, so long as we are dealing with large values of n.

Examples:

• Summing a list of numbers:  O(n)  -- single traversal of the list
• Sorting a list by inserting first into a sorted rest:  O(n²) -- double traversal of the list  (a traversal to insert each element)
• Finding an element in a perfectly balanced binary search tree:  O(log(n))  -- height of a balanced tree is O(lon(n))
• Finding an element is a completely unbalanced tree, worst case scenario:  O(n)  -- all elements along one branch = linear structure.

© 2010 by Stephen Wong