WAVELET-BASED IMAGE COMPRESSION

Wavelet theory uses a two-dimensional expansion set to characterize and give a time-frequency localization of a one-dimensional signal. Founded on the same principles of Fourier theory, the wavelet transform calculates inner products of a signal with a set of basis functions to find coefficients that represent the signal. Since this is a linear system, the signal can be reconstructed by a weighted sum of the basis functions. In contrast to the one-dimensional Fourier basis localized in only frequency, the wavelet basis is two-dimensional - localized in both frequency and time. A signal's energy, therefore, is usually well represented by just a few wavelet expansion coefficients.

1. Generated from a single scaling function or wavelet by scaling and translation
2. Satisfies multiresolution conditions. That is, if the basic functions are made half as wide and translated in steps half as wide, they will represent a larger class of signals exactly or give a better approximation of any signal
3. Efficient calculation of the DWT. Lower resolution coefficients can be calculated from higher resolution coefficients by a tree-structured algorithm known as a filter bank.

where the two-dimensional set of coefficients a_j,k is the DWT of f(t).

As the index k changes, the location and scaling of the wavelet moves along the time axis. As the index j changes, the shape of the wavelet changes in scale. As the scale becomes finer (j larger), the time steps become smaller. Both the narrower wavelet and the smaller steps allow a representation of greater detail or resolution.

In order to use the idea of multiresolution, a scaling function j (t) is used to define the wavelet function.

A two-dimensional family of functions is generated from the basic scaling function by scaling and translation.

The spans of the various scaling functions are nested, and after some linear algebra the recursive scaling function can be rewritten as:

where the coefficients h(n) are a sequence of real or complex numbers called the scaling function coefficients and the root two maintains the norm of the scaling function.

The wavelet function can then be represented by a weighted sum of shifted scaling functions

for some set of coefficients h₁(n).

There are five displays that show the various characteristics of the DWT well:

1. Time-domain. This, however, gives no information about frequency or scale.
2. Three-dimensional plot c(k) and d_j(k) over the j, k plane.
3. Time functions f_j(t) at each scale by summing over k so that









4. Time function f_k(t) at each translation by summing over k so that







5. Partitioning the time-scale plane as if the time translation index and scale index were continuous variables. (a.k.a. tiling the time-frequency plane)

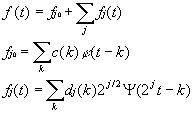
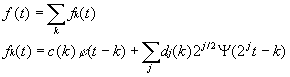
Wavelet analysis produces several important benefits, particularly for image compression. First, an unconditional basis causes the size of the expansion coefficients to drop off with j and k for many signals. Since wavelet expansion also allows a more accurate local description and separation of signal characteristics, the DWT is very efficient for compression. Second, an infinity of different wavelets creates a flexibility to design wavelets to fit individual applications.

[back to main page]