Reverse Link
- Pseudo-Random Numbers
Because transmitters for
this scheme are spatially distributed throughout an area (the cell), they
cannot be synchronized and thus cannot be perfectly orthogonal. CDMA uses sequences of pseudo-random
(essentially random, but computer generated in a repeating pattern) bits as
codes for the reverse link. Several
criteria are necessary for the selection of a set of pseudo-random numbers,
which are carefully determined when designing a CDMA system. In order to work in lieu of true orthogonal
codes, these sequences must:
1)Contain approximately
equal numbers of zeros and ones
2)Be approximately
orthogonal to other codes
3)Be approximately
orthogonal to themselves when delayed/shifted
4)Be easy to generate
- Gold Codes
Gold codes are specific sequences
of pseudo-random numbers that can be generated using two feedback shift
registers, and satisfy the above criteria.
A shift register is a digital logic structure where bits are shifted
serially through a chain of memory cells.
A feedback shift register is a shift register structure that uses a
modulo 2 addition on some of its bits to produce the bit fed into the input of
the structure. Most devices that use
Gold codes use two of the structures, each adding a different subset of its
bits to produce its feedback input. The
output of these two feedback shift registers is added (modulo 2) to produce the
Gold code, which repeats with a sequence length less than that of the two
sequences being added to produce it.
Different Gold codes can be produced by shifting the output of one of
the feedback shift registers relative to the other; adding them produces a
completely different sequence.
- Correlation and Orthogonality
The criteria for desirable
pseudo-random sequences specify much about “approximate” orthogonality, but the
meaning of such a statement is not necessarily intuitive. A degree of orthogonality between two
sequences can be measured using a statistical tool, cross-correlation. A value of zero indicates actual
orthogonality; our measurements are normalized so that a value of one indicates
identicality, the complete lack of orthogonality. To select Gold codes, cross-correlation of two candidates is
calculated for all possible shifts, or phases, of the two codes, to account for
all possible reception patterns that could arise with two distinct transmitters
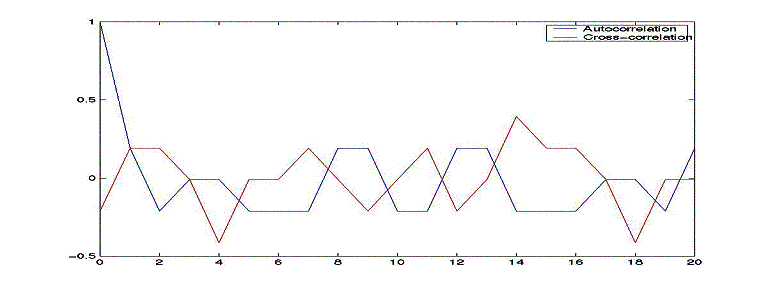
each using one of the codes to transmit to the same tower. A “good” set of codes will have
magnitudes(positive or negative) of cross-correlation much less than one for
all shifts. In an urban environment, a
tower will frequently receive multiple copies of the same signal delayed
because of different path lengths from the signal reflecting off of
buildings. In order to minimize
interference from the delayed signals, a “good” code will have low values of
autocorrelation (cross-correlation with itself), for any shift other than zero,
where it is by definition one. The plot
below shows the correlation data for two of the codes used in our experiment;
these codes are considered “good” for the code length that we used (21 bits).
Results
of Reverse Link Experiment
©2001 Kyle Bryson, Alison
Chen, and Allen Wan