Differential pulse-code modulation is a technique in which the derivative of the signal is quantized. When signal changes between sample periods are small, the quantizer's word length can be reduced. With very high oversampling rates, the changes between sample periods are made very small, thus the quantizer can be reduced to low-bit. A 1-bit DPCM encoder is known as a delta modulator (DM, delta). In other words, DM codes the differences in the signal amplitude instead of the signal amplitude itself. Another name for DM is pulse width modulation (PWM).
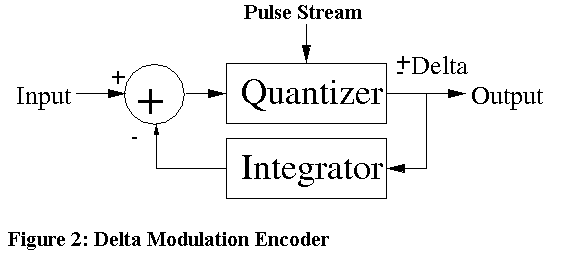
Figure 2 shows a delta-modulation encoder; it is known as a single integration modulator. The input signal is compared to the integrated output pulses and the delta (difference) signal is applied to the quantizer. The quantizer generates a positive pulse when the difference signal is negative, and a negative pulse when the difference signal is positive. This difference signal moves the integrator step by step closer to the present value input, tracking the derivative of the input signal.

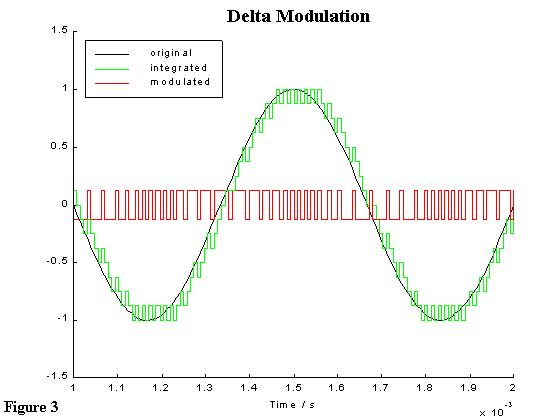
Considering a 1.5 kHz sinusoidal input signal, as an example, with maximum amplitude 1 and deltaV to be 0.0625, the sampling is equivalent to 4-bit quantization i.e. L=16. To achieve a bit rate equivalent to 4-bit quantization with 4 kHz sampling rate an oversampling ratio of 16 is needed i.e. 64 kHz (16 x 4kHz). Figure 3, shows a MATLAB simulation at 32 times oversampling. As seen the output of the integrator tracks agreeably the input signal.
As explained earlier, filtering is critical in oversampling in order to avoid the unwanted effects of aliasing and distortion. Having this in mind the output of the delta modulation (after the integrator) has to pass through a low pass filter in order to attenuate high frequency unwanted signals. Figure 4 is a MATLAB simulation which shows the effect of not using such a filter in 16 times oversampling of the signal used in Figure 3. As seen the modulated signal hardly tracks the actual input signal and as the integrated signal is shifted due to the effect of aliasing. Thus a lot of distortion is introduced and the reproduced signal at the demodulator will not resemble the original input signal (there is also no way to recover it).
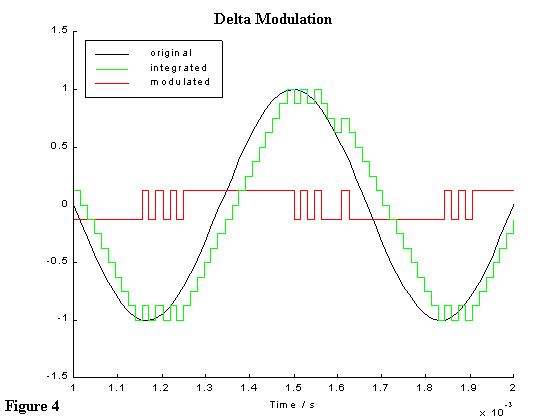
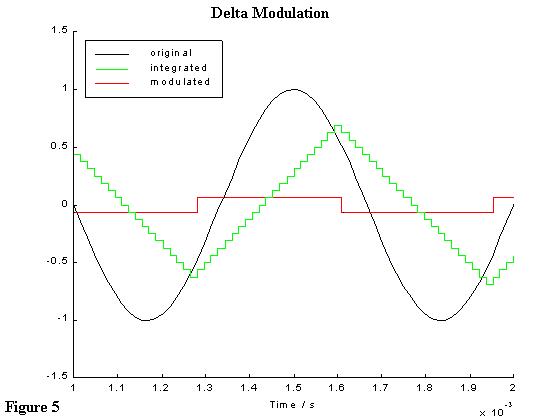
Figure 5 shows the importance of choosing the right oversampling ratio or the size of DV (which determines L, the number of quantization levels). If the size of the deltaV or the oversampling ratio is relatively low to the required values, a slope overload occurs. Choosing a deltaV of 0.125, double the previous deltaV=0.0625, there is an equivalence of 3 bit quantization, that is L=8. The oversampling ratio should be 32 (double the previous of Figure 3 to achieve a sampling rate of 4KHz). To show the effect of using a lower oversampling ratio than the actual required, Figure 5 shows an oversampling ratio of 32; the overload slope (signal changes to fast for the modulate signal to track) is inevitable.
In real CD player technology that requires a 16-bit word 1-bit PWM encoding, the 1-bit modulator will have to perform 2^16 toggles per conversion period. With a sampling frequency of 44.1kHz this would demand a toggle rate of approximately 2.89GHz (44.kHz x 65,636), plus some other bits for error correction and tracking. This is unrealizable with today?s technology, even in the most sophisticated VLSI digital signal processor micro-architecture. As the rate is slowed to accommodate hardware limitations, the noise level rises to unacceptable levels. Alternatively, there are two solutions to correct this problem: a bit reduction at high sampling frequency in order to output a low bit signal from a high-bit source or to increase the value of deltaV so as to lower the number of quantization bits. The first case will degrade the dynamic range of the sound in CD players and the second will make quantization noise more apparent due to its uniform distribution in the frequency band from dc to half the sampling rate. Obviously delta modulation is inappropriate in CD technology where high fidelity, high sampling rates and 16x oversampling are required; the quest remains.