Defocused Images

In this section, some basic theory on image defocusing will be addressed and then the group's image processing experiments will be discussed.

Theory

A common case of image blurring occurs when the camera is improperly focused. The image degradation system caused by an unfocused thin lens has the following Fourier transform:

H(u,v) = J1(ap)/ (ap) , where J1 is a first order bessel function, p = sqrt(u^2 + v^2), and a is the displacement (Sonka, et al).

This model was used to explore defocused images. The format J1(ap)/(ap) is also commonly expressed as a sombrero function, because its graph resembles a sombrero. The bessel function and the sombrero function can be related by the equation:

somb(p) = 2*J1(pi * p)/(pi * p)

H(u,v) = .5*somb(a*p/pi)

The inverse fourier transform of the sombrero is the cylinder function. The cylinder function is defined as:

cyl(r/d) = 1  ,  0 <= r  <  d/2 
           1/2,       r  =  d/2 
           0  ,       r  >  d/2 

where r = sqrt( x^2 + y^2)

The exact relationship between the cylinder function and the sombrero function is as follows:

  
cyl(r/d)  <=> .25*pi*somb(p), 
r = sqrt(x^2 + y^2), the variables used in the space domain, and
p = sqrt(u^2 + v^2), the variables used in the frequency domain.

Where <=> indicates the zero order Hankel transform, which is the Fourier transfrom in polar coordinates. The scaling property for the 2D Hankel transform is the following:

f(r/b) <=> |b| ^ 2 * F(b*p)

Using the scaling property with the transform of the sombrero function, the defocusing system can be described as:

  2*cyl(r*pi/a)*pi/(a^2)  <=>  J1(ap)/(ap)
       
       therefore h(r) = 2 * cyl(r*pi/a)*pi/(a^2)

With the above equation, image deblurring can be represented not only as a multiplication with a sombrero in the Fourier domain, but also as a convolution with a cylinder in the space domain.

Because the image processing in Matlab uses discrete steps of h(r), then the discrete Fourier transform of the image will take on a periodic property. The images below represents the cylinder function h(r) and its discrete Fourier transform, the digital sombrero at a = 30.

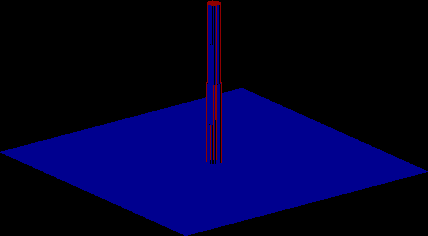
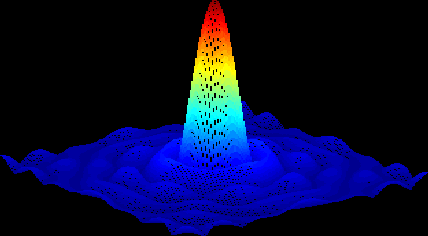
Both the cylinder function and the sombrero function are radially symmetric--both functions only depend on the radius, and do not depend on the angle from the origin. This circular property becomes obvious when circular images pass through these filters

Parallels between linear motion blurring and lens defocusing

Recall that linear motion blurring uses a rectangle function in the space domain and a sinc function in the Fourier domain to degrade the image. Similarly, lens defocusing uses a cylinder function in the space domain, and a sombrero function in the frequency domain for blurring. The cylinder function is much like a rectangular function in that they have a prism shape with different bases. The base for the rectangular function is obviously, a rectangle, but the base for the cylinder function is a circle. In the Fourier domain, the sombrero function can be described as a circular sinc function, with radial symmetry instead of the rectangular sinc's planar geometry.

Experiments

A Matlab m-file called defocus5.m was used to create h , the cylinder function and H , the sombrero function. Next, a circle image was created to test the blurring function. The results were shown below with varying values of a:

Left: original circle, right: circle defocused at a = 10.

Left: a = 50, right a = 100

Notice as a increases, the image becomes more and more blurred. Also note that the blurring images maintain their circular properties. This is due to the radial symmetry of the cylinder and sombrero function.

Topics