DSP Methods for Blur Reduction

Iterative Blind Deconvolution Performance Analysis

Our implementation of the Iterative Blind Deconvolution (IBD) algorithm (IBD algorithm, in Matlab) takes 6 parameters: the blurred image, the number of iterations, the size of the PSF, the noise constant (between 0 and 1; larger values for noisier images), the original image estimate, and the finite support. The noise constant is used in the Wiener filter-like operation of each iteration.

In running general tests, we noticed several points. First, we wrote a function which set the initial PSF estimate to a Gaussian PSF instead of an impulse (IBD with Gaussian PSF estimate, in Matlab); however, we did not notice any appreciable difference between the results of it and those of our standard algorithm. Also, we noticed that if the finite support reaches the edge of the image, substantial distortion can occur. Therefore, we always either padded the image and finite support, or just set the finite support to smaller than the image.

To test the performance of our algorithm, we started with a simple line drawing which we created for our group logo. We then blurred it and applied the IBD algorithm in several different ways.


Test I

First, we applied a 5 x 5 pixel Gaussian point spread function, and gave the IBD the following parameters: We ran the IBD with these parameters for 1, 2, 3, 4, 20, and 40 iterations.

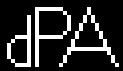
Original and Blurred images

Image after Iterations 1 and 2

Image after Iterations 3 and 4

Image after Iterations 20 and 40

In this case, the algorithm is quite sucessful.


Test II

We applied a 15 x 15 pixel Gaussian point spread function, and gave the IBD the following parameters: We ran the IBD with these parameters for 1, 2, 3, 4, and 5 iterations.

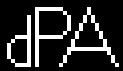
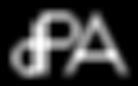
Original and Blurred images

Image after Iterations 1 and 2

Image after Iterations 3, 4 and 5

Here, the algorithm shows a flaw: it sometimes fails to converge. This means that the user of the program must look at each image produced and manually choose the best one. Still, there is noticable improvement at some iterations; the best we saw in this case was after the 3rd iteration. In particular, notice how the program separated the vertical lines of the d and P, which were merged in the blurred image.


Test III

We speculated that the large PSF used in the deconvolution prevented the algorithm from converging. We wanted to examine the effects of using too large of a PSF in the deconvolution, so we went back to a 5 x 5 pixel Gaussian point spread function to cause the blur, then gave the IBD the following parameters: We ran the IBD with these parameters for several iterations; the first 3 are shown here.

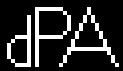
Original and Blurred images

Image after Iterations 1, 2, and 3

The results confirm our suspicion: using too large of a PSF estimate produces substantial artifacts outside the image, which will prevent convergence.


Test IV

Since overly large PSF estimates can prevent convergence, we wanted to examine the effect of using a PSF which is smaller than that of the blur function. If this were to be effective, there would be no need to use a large PSF and risk lack of convergence. This time we used a 15 x 15 pixel Gaussian PSF and used these parameters: We ran the IBD with these parameters for up to 5, and 20 iterations.

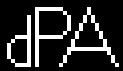
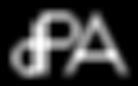
Original and Blurred images

Image after Iterations 1, 2, and 3

Image after Iterations 4, 5, and 20

Unfortunately, this does not provide any enhancement.


Test V

Next, we wanted to see how the IBD works for a photographic image. We applied the 5 x 5 pixel Gaussian PSF to an image of a pygmy owl, and gave the IBD these parameters: We ran the IBD with these parameters for 1, 2, 3, 4, and 20 iterations.

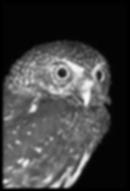
Original and Blurred images

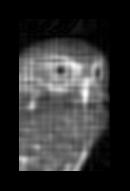
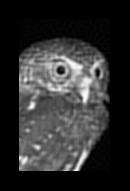
Image after Iterations 1, 2, 3, and 4

Image after Iteration 20

Here, the algorithm is quite sucessful again.


Test VI

All our tests so far have been in the fairly artificial case where the blur was applied mathematically by us, which is not a good real-world generalization. We wanted to see how the IBD works for a photographic image with "real-world" blur. We took a blurry image from an album cover, and gave the IBD these parameters: We ran the IBD with these parameters for 1 iteration, and saw a problem.

Original (Blurred) image

Image after Iteration 1

Apparently, the fact that we are using an constant-valued estimate is causing the filter calculation on the first iteration to darken the whole image.


Test VII

To solve the above-mentioned problem, we give the blurred image itself as the image estimate. We ran the IBD with these parameters for 1 iteration, and did not have the darkening effect which we previously noticed; however, there was also almost no noticable sharpening effect. We show here the image after 20 iterations. As it turned out, the image after that many iterations was again somewhat darkened, so we increase the intensity of all pixels by 2, and clipped the values to the maximum before the brighten.

Original (Blurred) image

Image after Iteration 20

Here, the sharpening effect is fairly noticable, particularly at the white- black intersections (look at The Edge's hat).


Test VIII

Since we don't know the size of the degrading filter, we also tried to sharpen the album cover image with a larger PSF. Again, after 20 iterations, we needed to brighten the image, this time by a factor of 3 (and again clipping the maximum value to the previous maximum).

Original (Blurred) image

Image after Iteration 20

The results are fairly similar to those from using a PSF size of 3. This gives an encouraging indication that the algorithm is not excessively sensitive to the PSF size.


Test IX

Finally, since we got good results in photographs using the blurred image as an estimate, we decided to try this with the logo image blurred with the 15 x 15 Gaussian PSF. We ran the IBD with these parameters for up to 5 iterations.

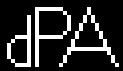
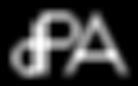
Original and Blurred images

Image after Iterations 1 and 2

Image after Iterations 3, 4 and 5

These images are worse than those where the estimate was merely a box; this indicates that the estimate should be chosen carefully.


Inverse Filtering Page
Main Page