Image Processing - Blind Deconvolution

The techniques that have been discussed so far have been concerned with inverse filtering or deconvolving an image given the point spread function. Blind deconvolution on the other hand does not assume any prior knowledge of the image or the point spread function, hence, we can see how it can be lot more useful in practical situations. Say we have a degraded image g(x,y) which is just some image h(x,y) convolved with some point spread function, f(x,y). So we have : g(x,y)=h(x,y)*f(x,y) (for now we ignore the noise factor).All we have to start off with is the degraded image.

The Iterative Blind Deconvolution Algorithm (IBD) starts with an initial estimate of the restored image, an initial estimate of the PSF restoring the image is by making an initial estimate of what the psf and image are. In the specific algorithm that we implement we assume that h is a 2-D impulse as shown below:

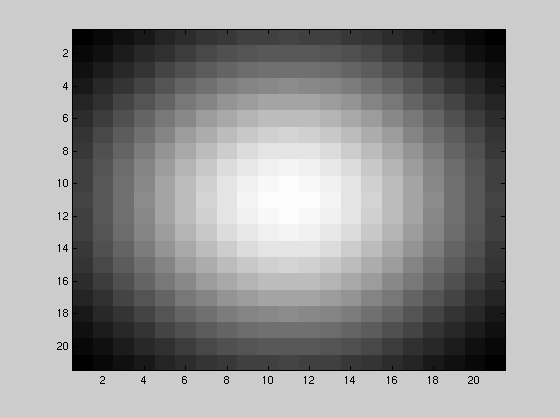
We normally used a gaussian point spread function such as the one shown below (21x21 point PSF) to blur the image :

One of the constraints that we apply to the image is that of finite support. Finite support basically says that the image does not exist beyond a certain boundary (this would be a valid estimate if we knew that the real image did not exist outside this region. If the image estimate appears outside of this boundary then we set it to the background value. The algorithm that we implement is known as iterative blind deconvolution (IBD). The block diagram of this is shown below :

The first set of fourier constraints involve estimating the PSF using the FFT of the degraded image and the estimate of the PSF :

                            _
                 G(u,v)conj(F(u,v))
Hk(u,v)= _______________________________
            _                  _ 
           |F(u,v)|^2 + alpha/|H(u,v)|^2

                            _
                 G(u,v)conj(H(u,v))
Fk(u,v)= _______________________________
            _                  _ 
           |H(u,v)|^2 + alpha/|F(u,v)|^2

The blur constraints that are applied are from the assumption that we know, or have some knowledge of the size of the PSF. Therefore, if we get anything outside of this boundary we set it to zero.

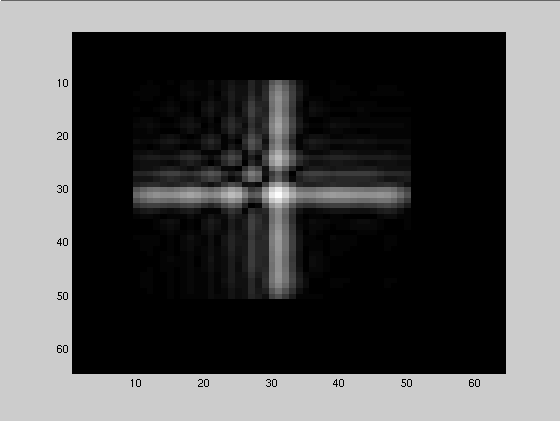
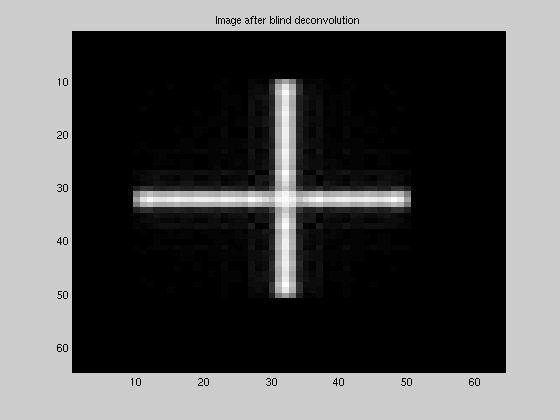
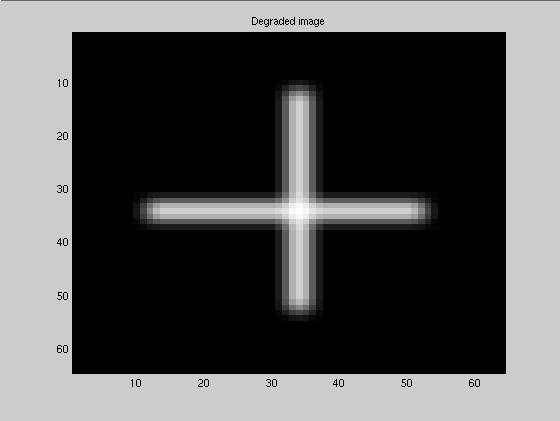
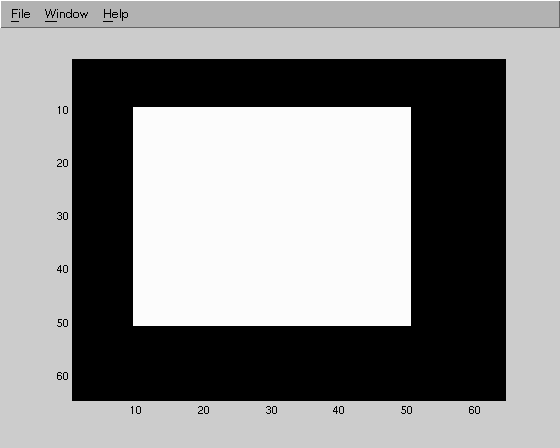
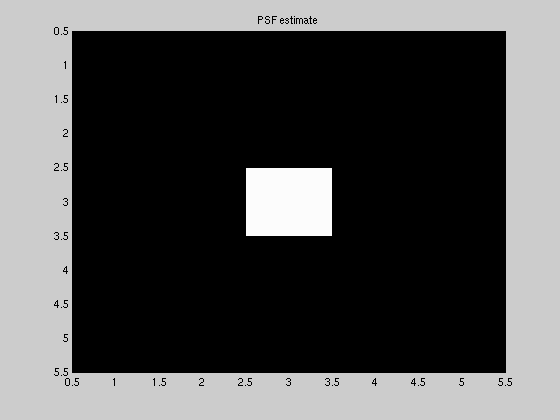
Implementation -Iterative blind deconvolution (IBD)

The IBD algorithm implemented in matlab.