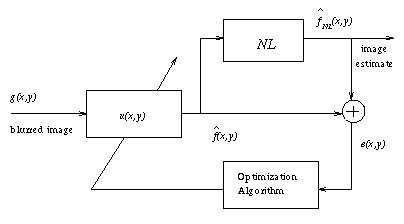
After working with the IBD algorithm for a while, we looked into other options, including Simulated Annealing, NAS-RIF, and higher order statistics methods. The only algorithm that could be implemented in a relatively simple manner was the NAS-RIF.

The NAS-RIF was developed to deal with the problems that the IBD method has with convergence and uniqueness[1]. It is not as restrictive as to what form the PSF must take, but does require that is be absolutely summable(BIBO). The NAS-RIF algorithm converges far better than its IBD counterpart, but performance in a noisy environment leaves something to be desired. NAS-RIf also has a big computational advantage over the IBD. The time it takes to process an image is proportional to square of the filter size, unlike the IBD where it is proportional to the square of the image size.

The algorithm calls for minimizing the error between the filtered image estimate and the expected qualities of the image, such as nonnegativity and finite support. We are using a version called steepest descent, that pushes the filter, u, straight toward what the optimal value is expected to be. There is a 'cost function' J that turns the error into something useful, and the gradient of J is the amount that we change u. Got it?

Say we have a blurry image(g), and want to clean it up. We know a few things about the 'real' image(f) - the one we want. It's so and so big, it has no negative values, it's this bright, and has a background color of such(bgcol). With this information, we compare the blurry image to what we expect, and (via the cost function,J) we get a matrix of values - values of the amount that we alter our 'deblurring' filter (u). Take a look at the function source bdecon4.m if you're curious.

The term that was used to change u looks something like this: (where sgn is sign(x) +/- and the gamma term is used if the bgcol is black, or 0)

Well, it all looks nice in theory. Our implementation seems correct, since the m-function converges, but the function doesn't sharpen very well. It might help to further restrict our 'expectation' functions, which would make J more accurate, and speed up convergence as well.

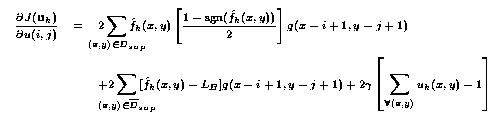
Examples:

original, blurred image


image with d=0.05 (< 5% change in u(k)-u(k-1)), d=0.01, d=0.001


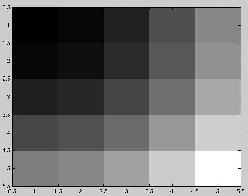
psf for (d=.05) 7x7 filter, 5x5 d=0.01, d=0.001(~500 iterations)


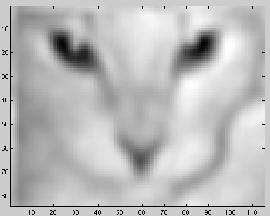
a fuzzy cat, a more evenly fuzzy cat.

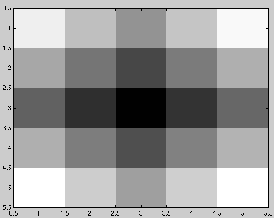
psf estimate from algorithm of fuzzy cat

Even though the output wasn't as good as I hoped for, its resolution does get slightly better as the algorithm converges.

Algorithm for blurring images with an asymmetric gaussian-based randomly-altered psf. defocus.m

Diagram and information reference:
1. Blind Image Deconvolution, Kundur and Hatzinakos

IEEE May 1996 Signal Processing Mag