Reverberation

Architects, engineers, physicists, and high-society music enthusiasts (i.e. artsy-fartsy types) spend large amounts of time, energy, and money designing rooms with very specific reverberation characteristics. Concert halls are some of the rooms in which controlling reverberation is most important. One of the difficulties of designing these halls is that their reverberation characteristics are constantly changing. The number of people in the hall has a pronounced effect on the reverberation characteristics, as does the apparel the people are wearing.(1) (Fur absorbs much more sound than vinyl, for example.) Thus, the halls must be designed to have desirable reverberation characteristics for a variety of situations. Many halls address this problem by installing acoustical banners along the walls. These banners of absorptive material can be deployed to reduce the amount of reverberation in a somewhat empty hall or retracted to increase the amount of reverberation in a full concert hall.

Reverberation has not always been such a significant consideration in architectural design. There was a time when the impact of a design on reverberation characteristics was not even considered. As some poor students and Harvard discovered, ignoring the powers of reverberation can be very detrimental...

So Sabine took on the challenge. He began taking measurements. He started with just how much sound reflection was in the room. He noticed that once the speaker stopped speaking that the sound continued for about 5.5 seconds. This is what made it so difficult to hear the lecturers because if they went on to the next sentence, the listener would still be hearing the beginning of the previous sentence! He used organ pipes, a stop watch, and some trained auditors as well as compressed air (to keep the level of the sound fairly even) and measured how long it took until you could no longer hear the sound.

This lead him to define the term "reverberation time"--the amount of time --> --it takes sound to die away, or to drop by 60 dB. This number comes from the fact that normal conversation is about 1 million times above the human hearing threshold. He also measured many other rooms on Harvard's campus to compare the "reverberation time" of each. He found that the reverberation time was largely dependent on the contents of the room as well as the building materials used to construct the room. He noted that "good" concert halls had a reverberation time of about 2 to 2.25 seconds (any less than this would cause the sound to seem "dry") and that "good" lecture halls should have a reverberation time of slightly less than 1 second.

He tested Fogg Lecture room by putting different materials in the room and covered the walls with a variety of materials. He found that when pillow cussions were added to the room, the reverberation time was significantly decreased. He also tested the room with various sized people and noted that the average person decreased the reverberation time by the same amount as slightly over six cushions. He also found that by putting felt on the walls significantly decreased the reverb time.

Sabine later helped in the design of Symphony Hall in Boston. Using his knowledge of the materials in the hall and the volume of the hall, he could come up with a fairly accurate prediction of the hall's reverberation characteristics.

Later, instead of using the unit of a seat cushion (as comfortable a unit as it was), researchers began referring to the amount of sound that would be lost out of a square foot open window (a perfect swallower of sound). This unit was named a Sabin (after our friend Sabine). One of the seat cushions he used is worth 0.7 sabins. One adult sitting in an audience is worth about 4.7 Sabins. But, as it turns out, a couple really is worth twice as much as one person (apparently Jill can't read); although this is a less interesting result, it renews our faith in concert hall ettiquite.(1)

As discussed above, reverberation is an important part of both playing and listening to music. Now that we are aware of its abundant importance to physical modeling, we must ask ourselves the fundamental question: "How do we model it?" There are two main ways to simulate the reverberation characteristics of a room: physical modeling and impulse sampling. Physical modeling is a mathematical process, which is along the same lines as the other segments of our project--physical modeling of a plucked string, and mathematical modeling of fractional delay. In order to model the reverberation time of a room via physical modeling, we must know several characteristics of that room; the most important are its size and shape, and the materials of which it is made. These values are used in a series of difference equations to determine the approximate reverberation time of the room. Impulse sampling is a more hands-on method. It involves simulating an impulse in the room of interest and recording the response to that impulse. This recording is assumed to be a fairly accurate estimate of the impulse response of the reverberation characteristics of that room. Thus, it can be sampled and used to filter sounds, creating an output that is at least very similar to the input sound played in the room of interest.

We decided to use the impulse sampling method to implement reverberation in our project. Initially, physical modeling seemed to be the more logical choice, since the project does focus on the physical modeling of music, but there were several factors that stood in our way. First, physical modeling requires a significant amount of detailed information about the room to be modeled (sizes, shapes, materials, etc.) that were not readily available to us and would require too much time with a ruler and a tape measure. In addition, a set of very complicated, intricate equations is required to obtain a highly accurate model. Though we were eager to learn all of the mathematical theory behind reverberation modeling, we did not have enough time to adequately tackle the subject. Impulse sampling allowed us to obtain the necessary information (an impulse response) relatively easily and to quickly transform the result into useful information we could manipulate to study reverberation.

We used a clap to simulate an impulse since it is the shortest sound we could make, and it is fairly loud. We wanted to sample a room that had noticeable reverberation characteristics and that exhibited the reverberation over a long enough period of time that we were able to hear and see "echoes" in the impulse response. We experimented with several different rooms including a Shepherd School practice room, Stude Concert Hall, and a Will Rice College shower. As we expected, the impulse response in the practice room showed very little reverberation. We hypothesized that the reverberation that did appear was due to the dilapidated piano that rang audibly for nearly a minute after each clap. The shower impulse response showed quite a bit of reverberation, but it occurred too quickly, and it was difficult to differentiate one echo from another. This result is likely due to the fact that the shower is very small, so the echoes reach the listener (or microphone) much more quickly than in a large room.

To borrow a concept from Goldilocks and the Three Bears, if the practice room was too dead, and the shower was too live, then Stude Hall was just right. We obtained an impulse response with distinct echoes. We would expect Stude to have a pleasing impulse response since it is a concert hall and was designed to to have a reverberation time that is pleasing for musical performances. We used a laptop computer to record the response that resulted when Bryan clapped in Stude Hall. Bryan stood directly in front of the stage and faced the audience to "perform" his clap. There were no people in the audience, and the acoustical banners were fully retracted. The microphone was placed immediately to his right, so we simulated the response as it would be heard by the sound emittor.

Because the recording equipment used was less than perfect, our impulse response exhibited some constant high frequency noise. This noise was probably due to the hum of the computer--Stude is designed to have no extraneous noise. We used a sound-editing algorithm in Bryan's midi software to remove the noise. The algorithm simply input a sample of the noise alone (a time interval during which we were not clapping), took an FFT of the sample, and then removed the frequency components corresponding to that FFT from the entire signal. This greatly increased our ability to see the reverberation peaks in the impulse response. 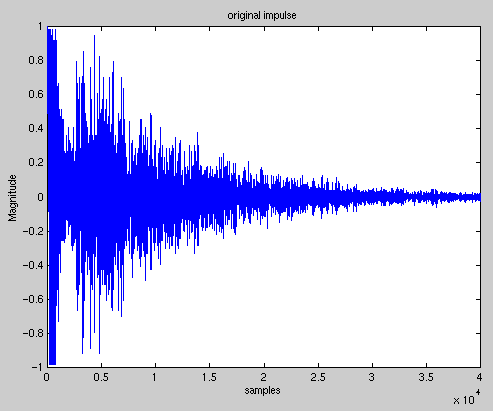The resulting noise-reduced impulse response is shown below:

The official reverberation time of Stude Hall is .75 seconds with the acoustical banners fully deployed and 1.3 seconds with the banners fully retracted. (3) Since we recorded our impulse response when the banners were retracted, we would expect our impulse response to drop by 60 dB in approximately 1.3 seconds. Referring to the above plot of the impulse response, we see that it has not quite dropped by 60 dB at the right edge of the graph. Our sampling frequency is 44.1 kHz, so the 4*10^4th sample (at the end of the graph) corresponds to approximately one second. Thus, the impulse response appears to die out in the 1 to 1.5 second range, which is consistent with the 1.3 second time given by important, official, musical people.

We used this noise-reduced impulse response to create a Matlab function which inputs a sound vector and outputs a vector of what the original vector would sound like if played in Stude Hall. The development of that function, finaldelay.m, is described below.

Here's where we attempt to explain all that we did in our code. I really hope it all makes sense.

At a high level, the reverb code performs a convolution between the sampled impulse response we got from stude and the input. However, since the input size is unbounded, and the impulse response is finite, we used a circular delay line to make things go faster.

The circular delay line is of size N, where N is the length of the impulse recorded. The delay line reads in samples from the input, and keeps them around until N samples later. The output simply is the sum of the elements in the delay line scaled by the values in the impulse array. For an efficient implementation of the circular delay line, the delay line was kept as an array, with indexes pointing into the array for each of the impulse points. These pointers will move down the array, and when they reach the end, they loop around. The pointer corresponding to the initial value in the Impulse array is where the input is copied into. Since the delay line is the length of the Impulse, when we go to copy in the next value, we are assured that the value being written over is a value which is no longer needed. This pointer movement is implemented by adding one to each of the pointers, and using a mod of the length of the line to loop around pointers which have reached the end.

For each sample we output, we need to do an add and multiply for each point in the impulse. Thus, the complexity of the algorithm would O(length(x)*length(Impulse)). Since the Impulse length is constant, this is a linear O(n) algorithm. However, it runs faster if there are fewer points in the impulse. Thus, we take only a subset of the points in the recorded impulse. Good time/quality tradeoff is achieved by taking every 50 points. So for the index array I_ptr, each pointer will be pointing to samples in the delay line which are 50 samples apart.

When we recorded the clap in stude hall, we had the gain on the microphone set fairly high, so that we could record the returning echos. With the gain this high, the initial clap clipped, so we can't tell the relative magnitude of the initial pulse with the rest of the file. We took a value which sounded best, and ended up scaling the first impulse to be 5.

The Matlab code for finaldelay.m and convert.m is provided below.

%x = doit('mary.snd');  % reads in sound output of pluck.cc, scales it, 
                        % and plays it
x = auread('name.au');  % reads in the sound file name.au

%  We either read the mary.snd file or the name.au file. We can change this.

plot(x);  % plot the original sound file

a = auread('stude-clap.au');   % read in what we're going to sample as 
                               % our impulse response

a = a(4596:length(a));  % cuts out information before the clap
a(1) = 5;   % sets initial clap magnitude to 5 (guess of what we thought it was)

a = resample(a,8196,44100);  % resamples to 8K.

sr = 50;   % sets sample rate to 50. This can be changed
Impulse = convert(a,sr);   % samples at rate sr and creates an impulse response
                           % matrix of sample numbers and sample magnitudes

Impulse = abs(Impulse);    % takes absolute value of impulse response (easier
                           % to deal with)
    
Imp_Max = max(Impulse(:,1));
I_ptr = Imp_Max - Impulse(:,1) + 1; 

subplot(311);stem(Impulse(:,1), Impulse(:,2));  % plots sample number 
                                                % vs magnitude
subplot(312);plot(x)     % we again plot our original signal to compare later
               
Delay = zeros(1,Imp_Max);  % creates a vector delay of length of the maximum
                           % sample number

y = zeros(1,length(x)+max(Impulse(:,1)));  % output vector of length of signal
                                           % plus length of imp. response that
                                           % is initialized to zero.

for(sample=1:length(y))  % for loop to compute output

  if(sample < length(x) )  % if sample is less than length of input 
    Delay (I_ptr(1)) = x(sample);                             
  else 
    Delay (I_ptr(1)) = 0;  
  end 
  %create output
   y(sample) = sum ( Delay(I_ptr)'.* Impulse(:,2) );
  
  %move pointers 
  I_ptr=mod(I_ptr,Imp_Max)+1;
end

y = y/max(y); % normalize y to +/- 1 range so it can be played by matlab
  
subplot(313);plot(y)  % plot output

function [outmat] = convert(a, sr)

plot(a);
title('original impulse');
as(1) = a(1);
for (i=2:(length(a)/sr))
       as(i) = a(sr*(i-1));
end

figure;
plot(as);
title('sampled impulse');


for (i=1:length(as))
       outmat(i,1) = i*sr;
       outmat(i,2) = as(i);
end
figure;
plot(outmat(:,1), outmat(:,2))
title('outmat');

figure;
     
plot(outmat(:,1), outmat(:,2));

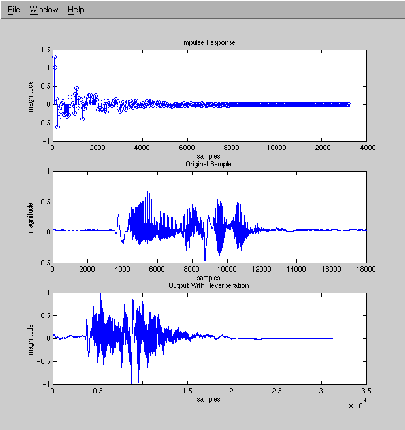
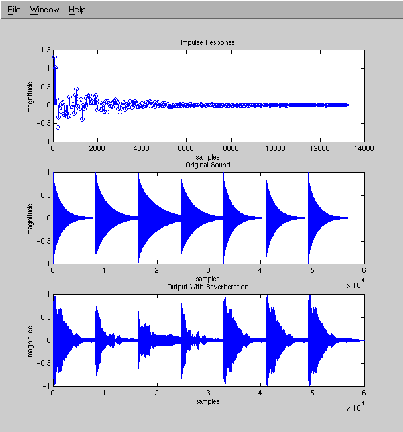
We used finaldelay.m to process two sound files. The first, name.au, was Vijay sharing a philosophical thought: "My name is Vijay." The second, mary.snd, was the first phrase of "Mary Had a Little Lamb" simulated using the pluck.c code. The results of both inputs are shown below. Note that, after processing via finaldelay.m, the vectors are sampled at a rate of 8 KHz, not 44.1 KHz. Thus, all sound vectors shown on the graphs below have a sampling rate of 8 KHz.

The bottom plot on each image shows the output signal of finaldelay.m. The reverberation is most clearly visible in "Mary Had a Little Lamb" due to the periodic nature of the input signal. It is interesting to notice the significant amount of time that it takes each of the impulse responses to die out. Reverberation really does exist!

We were very pleased with the results of our Matlab implementation, but there are few imperfections that should be addressed in order to maintain our engineering ethics (one of the ABET 2000 requirements). First, we should note that a clap is not a perfect impulse response. A perfect impulse response would be infinitely narrow in time and contain all frequencies. A clap is very short and has many frequencies, but it still has some finite length and a pitch and is therefore not a perfect impulse. This is apparent in our sounded output, since it has some smearing and immediate reverberation at high levels (due to the length of the clap).

Another point that should be noted is that we obtained the impulse response of Stude Hall at one particular location: directly in front of the center of the stage. The impulse response will be slightly different at every location in the hall, since the reverberations are coming from several locations and directions. Finally, we should note that we are uncertain about the maximum amplitude of the initial clap (impulse). Because the original clap clipped, we were required to estimate its magnitude. We did this by listening to the output for different clap magnitudes and qualitatively choosing the most accurate one. This may have resulted in echoes in our simulation that are slightly louder or softer than the actual Stude echoes, but it does not affect the "meat" of our results.