Linear prediction

There are various kinds of formulations for linear prediction problem. Two important algorithms are Levinson algorithm and Burg algorithm. Although a bunch of functions to solve AR model problem can be found in matlab (such levinson, ar, lpc,…) the interfaces are always too complex to be efficient. (Unfortunately, we found many mat-lab tool-box functions written in a badly style with confusing defined data-structures, e.g. the wavelet tool box too.) We also believe that our own implementation of algorithms will help much more than just calling these functions. So in this project, we first try to understand these algorithms and then wrote our own levinson and burg program in a concise style. We hope this study more helpful for the deeper understanding of the literature. Moreover, the expertise built through this work can help us easily write a C or asm language program for real-time application. We also carried out comparisons of these two algorithms.

Levinson algorithm

In a p-th order forward linear predictor, the current sample of speech is predicted from a linear combination of the p-past samples. Levinson algorithm is achieved by minimizing the MSE of forward prediction error. And then by applying the Toeplitz feature of the auto- correlation matrix, a fast algorithm based on order-recursion is derived by levinson. The recursion is formulated as Fig:

We have derived the algorithm in our homework, we omit the details here. Source code can be found in the software packet. Because this algorithm is based on the solution of a Toeplitz autocorrelation matrix, it is also called autocorrelation method.

Burg Algorithm

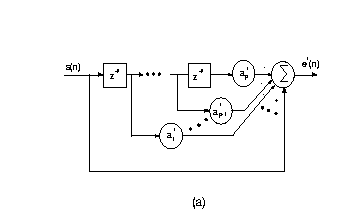
Burg algorithm is a kind of forward-backward prediction. Based on the Levinson recursion and this prediction, we derived the following recusive computation:

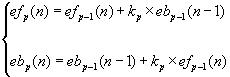
In which the reflection coefficients are computed with this expression:

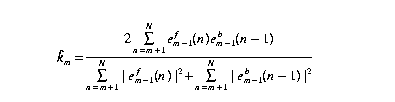
The figure below shows a clear diagram of the recursive computation of Burg algorithm.

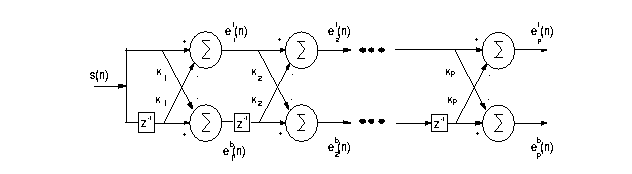
(b)

We carried out a comparison between these two algorithms. Summarily, they have the following differences:

  1. Computation form: Note that Levinson algorithm has a direct form while Burg algorithm has a Lattice form. In burg algorithm, the reflection coefficients can be computed directly in different stages without the computation of the prediction filter coefficients. We also highlight here that the lattice form is a representative direction in filtering theory.

  2. Although both algorithms guarantee stability in theory, in practice, Levinson is more sensitive than Burg. Some kinds of preprocessing (preemphsizing, windowing) will improve the performance. But for burg, this procedure can be saved.

  3. For Levinson algorithm, the computation of Autocorrelation function is required. In burg algorithm, there is no need for this.

Order Selection

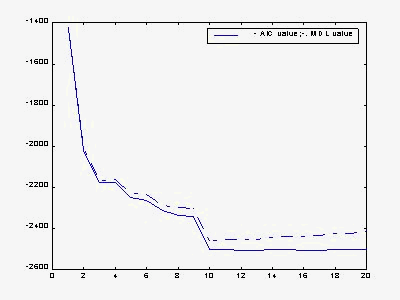
Order selection is very important for AR model. We did experiments for both levinson and burg with AIC and MDL criterion. AIC is expressed as AIC(k)=Nln(MSE(k))+2*k , MDL is computed as MDL(k)= N* ln(MSE(k))+k*ln(N); The left figure below is the result of levinson and the right burg. Solid line is AIC and dashed line is MDL. From the result, we found that MDL has a clearer valley for both levinson and burg algorithm. AIC tends to overestimate the order since the valley is not clear even for order 20. This means that MDL has a better performance in the selection of order. This maybe because MDL considers the number of bits in the second term. We can also see clear from the result that an order 10 is enough for voiced while order 4 looks good for unvoiced speech( result not shown here). That is why we can typical LPC vocoder LPC-10. We also found that the cost function decreases faster than Levinson. This may also support the strength of Burg over Levinson.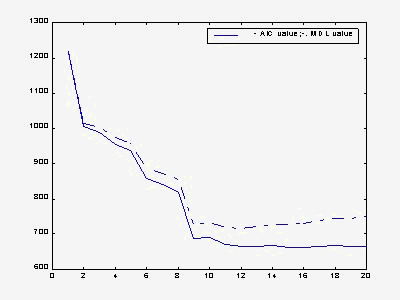

Application of LPC parameters

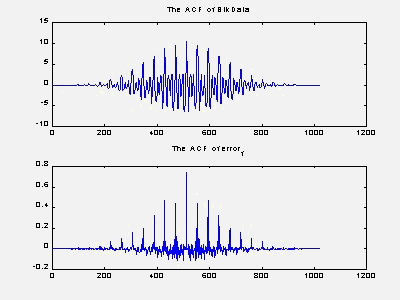
We mainly studied features of the predictor error. The ACFs of both original signals and residual are plotted for one section of typical voiced speech. It is clear that the ACF of residual shows more significant periodics than original signal. This is because the residual has been reduced the long-term correlation and made more whitened. So it may be used for pitch detection with better performance.