Image Enhancement

Motivation
Regardless of the number of angles we use to calculate projections or the number
of detectors we use in our array, we are always going to introduce artifacts
into our image reconstruction. This is due to quantization noise on
the projection inputs, interpolation errors between cartesian and polar
coordinates, and the discretization of a continuous space
into digital quantities. Image errors can also be introduced by the shifting
of the patient while the projections are being recorded, or by the rhythmic
expansion and contraction of internal organs due to their function.
Moreover, even though we may be able to improve
our image quality with a larger number of projections, the patient would
most likely prefer not to have a large x-ray exposure. Thus, if we can use image restoration to get the same quality of
reconstruction using a lower number of projection angles,
the patient benefits through both lower cost and health risks.
Five methods were used to try to improve the quality of our reconstructions.
They are all post-reconstruction filters.
The first two methods were derived simply by looking at obvious artifacts
in our reconstructed images. To begin with, some of the pixels in the
reconstructed image had negative values. The cause of these
negative values is due to computational roundoff and Gibb's
phenomenon in the discrete Fourier transform filtering. This would be
akin to having negative x-ray absorption in our detectors, which is physically
impossible. There is no way to absorb a "negative" amount of x-rays. We, therefore, set all negative values in our reconstructed image to zero using
zeroneg.m.
Second, for images derived using a low number of projection angles, we saw a
lot of artifacts located outside the thoracic cavity. Artifacts can easily be seen outside the chest region in images with 250 or
less projection angles. We removed these by setting to zero all
elements less than a threshold. We felt justified, because in practice
we know the absorption amounts of different tissues in the body, so we can
assume pixels with much lower absorption values are artifacts of the
reconstruction process.
The next two enhancement methods we used came from general image processing
ideas. The first is median filtering. Median filters have the
advantage of smoothing images while retaining edges to a large extent.
Median filters are scalable
and have constant additivity, but are nonlinear, so they are hard to
analyze. However, they are easy to implement, and are extremely useful
in removing impulsive noise [1]. A median filter can have any shape and will
scan over the entire image, with each output point corresponding to the
median of the data located in the filter at each input point. We used
a 3x3 median filter and increased the size until there was too much
smoothing. MATLAB has a built-in function medfilt2.m that performs
this operation.
The second general enhancement technique we used was Wiener filtering.
Wiener filtering consists of two frequency domain ideas. We begin by
assuming that the error in our image is due to some low pass blurring model
h, along with additive noise.
The first part of the filtering involves deconvolving our blurred
image by multiplying by 1/(fft(h(t))) in the frequency domain. Unfortunately,
inverting h(w) where the values are small (high frequencies) creates noise in the image. Wherever our SNR is high due to the additive noise, we suppress the inversion of our blurring filter by scaling it down. This is the
second component of Wiener filtering.
It turns out, however, that these
ideas are based in infinite impulse response filters and require a lot of a priori knowledge to implement (the
type of additive noise, the blurring model h, and the original
image statistics). We implemented a 2-D adaptive noise removal filter
built into MATLAB, wiener2.m. This function is space varying because
it uses a pixel-wise
adaptive Wiener method based on statistics estimated from a small area around
each pixel rather than trying to estimate the statistics of the entire image
[6].
The final enhancement technique that we attempted was derived after looking
at the type of error our reconstructions introduced. Figure 4.1
displays a 3-D plot of error versus spatial location for a typical image.
Theory
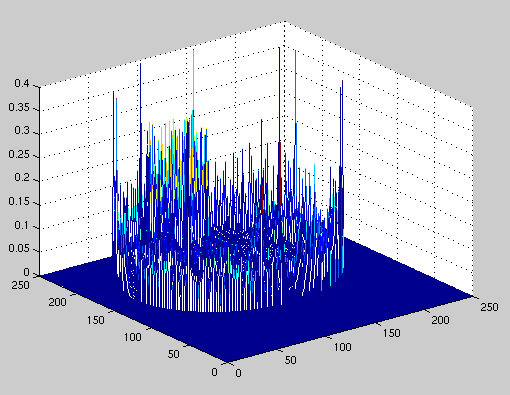
Figure 4.1 Error in image reconstruction
It can be seen from the above figure that most of the error lies at the outer
edge of the image. There are smaller peaks located at the edges of the
organs within the image. These peaks are smaller because the density
changes at the edges are smaller. Visually, these errors can be seen
on our results page as the blurring
of the edges in our reconstructed images. As such, we decided to perform
edge thinning on our images to make them look crisper.
We decided the most appropriate way to do edge thinning was in the wavelet
domain. The Haar wavelet transform performs sum and difference calculations
on the input image data. The actual transform is as follows:
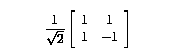 |
(4.1) |
This transform can be applied to adjacent horizontal points (paired off in twos), then adjacent vertical cells. The effect is that the upper, left quadrant of our transformed image will be the sums of the reconstructed image between adjacent points along both the horizontal and vertical axes (thus it will appear as a blurrier version of the image). The upper right quadrant will contain sums along the vertical axis and differences across the horizontal. The lower left quadrant will contain the sums along the horizontal axis and differences across the vertical, and the lower right quadrant will contain differences across both axes. An example is shown in Fig. 4.2 below, created by calling trans.m.

Figure 4.2 Reconstructed image after using the Haar wavelet transform
It can be seen from the figure above that the upper right quadrant picks
out vertical edges and the lower left quadrant picks out horizontal edges.
This capability is what prompted us to use the Haar Wavelet Transform for
edge thinning. We proceed by replacing the upper right quadrant with peaks
detected across each row to thin the vertical edges, and replacing the lower
left quadrant with peaks detected across each column to thin the horizontal
edges. This was done using rpeak.m in MATLAB. Then
the transformed image was inverted back to the spatial domain using
itrans.m. Note that the inverse Haar wavelet transform
is identical to the forward transform.
The results of these five enhancement techniques can be seen in Table 5.1 in the results section.