Practice with Graphs

Python Representation of Graphs

Today, we will develop code to work with graphs. Our first task is to choose a data representation. For the time being, we will simplify the matter by not allowing node labels and edge labels. Thus, we only need to represent graphs such as the following.

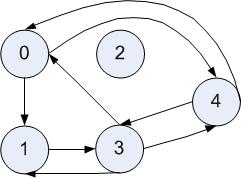
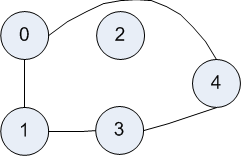
We can model both directed and undirected graphs with the following representation. A node is represented by its name. We can use numbers or strings for names. A graph is then represented by a dictionary mapping nodes to its successors, a list of nodes.

For example, to represent the directed graph above, we have

• directedGraph = {0: [1,4], 1: [3], 2: [], 3: [0,1,4], 4: [0,3]}
      

For example, whenever there is a directed edge from node A to a node B, then the dictionary maps A to a list that includes B. Furthermore, we can allow unconnected nodes. For example, there are no edges from node 2, so the dictionary maps 2 to an empty list of nodes.

Similarly, to represent the undirected graph above, we have

• undirectedGraph = {0: [1,4], 1: [0,3], 2: [], 3: [1,4], 4: [0,3]}
      

Our representation of an undirected graph lists each graph twice. If there is an edge from node A to node B, then the dictionary maps A to a list that includes B, and it also maps B to a list that includes A.

So, for the following graphs, give the corresponding Python dictionary representation.

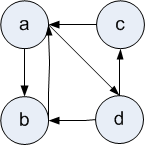
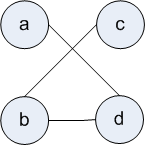
• directedGraph = {"a": ["b","d"], "b": ["a"], "c": ["a"], "d": ["b","c"]}
      

• undirectedGraph = {"a": ["d"], "b": ["c","d"], "c": ["b"], "d": ["a","b"]}
      

Examples of Building a Graph

Rather than defining graphs “by hand”, we typically define functions that create graphs of a certain type.

Directed ring graphs

Our first example will be to define a function that creates directed ring graphs. A directed ring graph looks like a big circle, with each node pointing to the next.

A directed ring graph of 3 nodes has how many edges? Can you draw or list them?

• Let's name the nodes 0,1,2.
  3 edges, one outgoing edge per node: 0 to 1, 1 to 2, 2 to 0.
      

More generally, a directed ring graph of n nodes has how many edges?

• n edges, one outgoing edge per node.
      

Define a function that takes n, the number of desired graph nodes, and creates a directed ring graph. The graph nodes will be named with the numbers 0…n-1. Thus, node 0 has an edge to node 1. Node 1 has an edge to node 2, etc. Node n-1 has an edge to node 0.

• Hint: You might want to use the “modulo” operator, %, which returns the remainder of x/y.

  def makeDirectedRing(n):
      """Returns a directed ring graph of nodes 0..n-1."""
      ring = {}
      for node in range(n):
          ring[node] = [(node+1) % n]   # Make a list of the one successor node.
      return ring
      

• But, here's a version without using modulo.

  def makeDirectedRing(n):
      """Returns a directed ring graph of nodes 0..n-1."""
      ring = {n: [0]}
      for node in range(n-1):
          ring[node] = [(node+1)]   # Make a list of the one successor node.
      return ring
      

Complete graphs

Our next example will be to define a function that creates complete graphs. A complete graph is simply one that has all possible edges. That is, each node has an edge to each of the other nodes.

A complete graph of 3 nodes has how many edges? Can you draw or list them?

• Let's name the nodes 0,1,2.  There are two ways to count.
  If we think in terms of directed edges, there are six, two per node:
  0 to 1, 0 to 2, 1 to 0, 1 to 2, 2 to 0, and 2 to 1.
  If we think in terms of undirected edges, there are three, i.e.,
  half as many: 0-1, 0-2, and 1-2.
  
  Note that our Python data representation doesn't distinguish between
  these two.
      

More generally, a complete graph of n nodes has how many edges?

• Directed: n(n-1).  Undirected: n(n-1)/2.
      

Define a function that takes n, the number of desired graph nodes, and creates a complete graph. The graph nodes will be named with the numbers 0…n-1.

• def makeComplete(n):
      """Returns a complete graph of nodes 0..n-1."""
      complete = {}
      for node in range(n):
          edges = range(n)        # Create an edge to every node...
          del edges[node]         # ...except itself.
          complete[node] = edges  # Add the edges to the graph.
      return complete
      

Example of Using a Graph

In later classes, we will discuss many things that you can do with graphs. The following is one simple example to get us familiar with working with the data structure.

The out-degree of a directed graph node is the number of edges from the node. Similarly, the in-degree of a node is the number of edges to that node. For example, in the following graph, the out-degree of node 1 is 1, while its in-degree is 2. Meanwhile, the out- and in-degree of node 2 are both 0.

When discussing undirected graphs, there is no distinction between out- and in-degree, and we just call it the node degree.

There are various reasons why we might be interested in the (out-/in-)degree of a node, or the average degree of the entire graph. As we've already seen, the average degree of a ring graph is one, while of a complete graph is n-1. The average degree gives us an measure of how well-connected the graph is — for example, the average number of Facebook friends. It helps us determine other properties such as whether the graph is “3-colorable&4dquo;.

Before we start writing any programs, it will be useful to think about some properties of out- and in-degrees.

Describe in English how to calculate the average out-degree of the nodes in a graph.

• We just following the definitions of out-degree and average.
  For each node, compute the node's out-degree, i.e., the size
  of the list graph[node], and add these values.
  Divide the total by the number of nodes, i.e., len(graph).
      

Describe the relationship between the average out-degree of a graph's nodes and the same graph's average in-degree.

• Perhaps surprisingly, they are the same!
  Since both averages are over the same number of nodes, compare instead
  the sum of the out-degrees to the sum of the in-degrees.  These sums
  are equal since each edge is counted towards one node's out-degree
  and towards one node's in-degree.
      

Write a program that returns the average out-degree of a graph.

• def averageOutDegree(graph):
      """Returns the average out-degree of the graph."""
      return float(sum([len(edges) for edges in graph.values()])) / len(graph)
      

Related Resources on the Web

• Networkx overview — We will discuss networkx later, but this page includes Python code to draw graphs defined as we have here.
• Wikipedia: Degree, Indegree and outdegree
• Webwhompers: Graph Theory — A similar introduction, except without the Python.