Home | The Problem | How TDS Works | Applications | Other Measurement Techniques | Future Projects
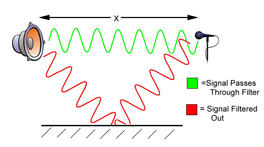
Since we are working in a "real-world" reverberant environment, any wave emitted by the loudspeaker will be reflected off surfaces in the room, we need a method that will consider only the "direct path" waves--those emitted only by the loudspeaker. In other words, we need to filter out the extraneous sounds that are contributed by the room--we need a way to accept only the direct wave from the loudspeaker into our microphone that is measuring the system response.

We accomplish this by creating a bandpass filter tuned to a given frequency, leaving the system on for the time it takes for the wavefront to reach the microphone from the loudspeaker, and then turning the system off. We then shift the loudspeaker to a new frequency, re-tune the filter to the new frequency, and then repeat.
Alas, we would like to test the loudspeaker system response for a given range of frequencies (say 20 Hz to 20 kHz, the range of human hearing). Using this system, we would need to repeat the experiment for every frequency in the range. We need a practical method to measure every frequency in a given range.
One way around this obstacle is to use a linearly swept sine wave (also called an FM chirp) as our input signal. A swept sine wave has the formula x(t) = sin(k*t^2), where k is called the sweep rate, and has units of Hz/second. The swept sine wave starts at zero frequency, and "sweeps" linearly upward toward higher frequencies.
Since our input signal sweeps, our filter must also sweep upward at the same rate. However, our filter must always sweep a certain amount of time behind the input signal. In other words, we must account for the time it takes for the emitted wavefront to reach the microphone. This delay is usually constant, given that the microphone and speaker do not move relative to one another. This delay is a time offset, but it is usually referred to as the frequency offset, since the center frequency of the bandpass filter is always slightly behind the frequency of the signal emitted by the speaker.
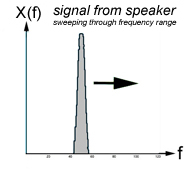
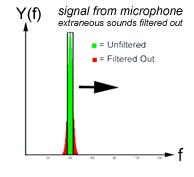
We can quantitatively determine certain variables within our system, including the time offset of our tracking filter and the bandwidth of the tracking filter. Assume that the speaker and the microphone are a distance X apart, and let Ft represent the pressure wave emitted by the speaker, and Fr be the pressure wave received by the microphone. The difference between the received and transmitted signal is:
Fr - Ft = [X (dF/dt)] / c .
Here, c is the speed of sound and dF/DT is the sweep rate of the signal (usually in Hz/second).
If our tracking filter has a bandwidth B Hz, then our sweep tone will travel some dX in space while within the bandwidth of the filter. Since our filter is not ideal, we must further define dx as the region in space where the signal power is at least half of its maximum value. We can call dx the space equivalent bandwidth, and we can relate it to bandwidth B, speed of sound c, and the sweep rate dF/DT
dx = B [ c / (dF/DT) ] .
We can further expand the concept of time delay spectrometry to measure the complete system response of a sound system, including the reverberant environment. We must simply slow down the sweep signal so that some of the acoustical scattering from the room surfaces leaks through our tracking filter. Essentially, our goal is to let the room reach steady-state equilibrium at each frequency before moving to a new frequency. By taking measurements at progressive time intervals, we obtain a plot of sound pressure as a function of both frequency and time.
Since we are assuming that our system is LTI, we may think of each reflecting surface as a loudspeaker image. Our system is a series of loudspeaker images, each system having its own unique transfer function. Each transfer function is the product of a spectral energy distribution from each surface, S(w) and a linear phase coefficient, e^(-jwt). The system response is the sum of all of these individual surface responses:
![]() .
.
The impulse response of the system is given by the Fourier transform of R(w).
![]() .
.
Now that we have the system response, we can obtain a response for any given input signal. This input signal is often called the program material, and is denoted by p(t) or P(w). In the time domain, the output for any given program source p(t) is the convolution integral of the program signal and the room impulse response:
![]() .
.
Note that this analysis is valid only for a given combination of speaker and observer. Our system response is not a general characteristic for a room but it is related to the "true" room response. In most practical situations, the system response given a stationary observer and loudspeaker system is all that is needed.
Home | The Problem | How TDS Works | Applications | Other Measurement Techniques | Future Projects