Main
Background
Methods
Results
Conclusions
Group Members
Method
Quick Links
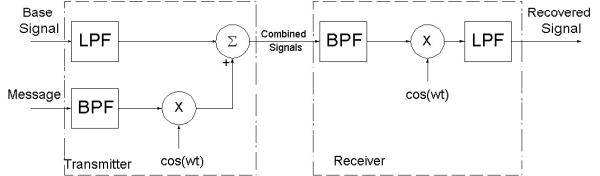
Block Diagram of Frequency Domain System
For a CD, the sample rate is 44.1 kHz which makes the highest
frequency without aliasing 22.05 kHz. Also, we noted that the
average peak frequency that an adult can hear is approximately 18
kHz, which leaves 4 kHz of frequency that is practically
"unused". We put this frequency range into use.
We begin with two signals, such as the ones below. These
will be called the "base", which contains the hidden message, and
the "message", which will be hidden in the base. The
spectrograms of two such signals are shown below.
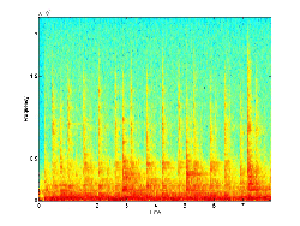
Base Signal |
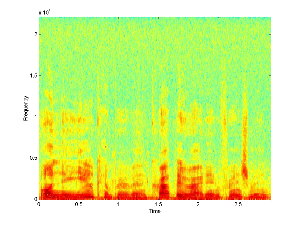
Message Signal |
Next, we take the base signal and lowpass filter it to 18 kHz,
which will clear up the upper 4 kHz. Following the example of
the telephone company, we will bandpass filter the message signal
from about 300 Hz to 3.3 kHz, which will be a small enough band
to fit in the upper portion of the filtered base. The two
filtered signals are shown below.
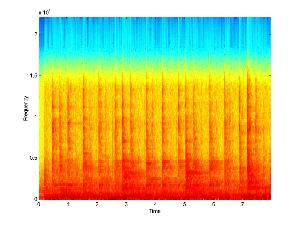
Filtered Base Signal |
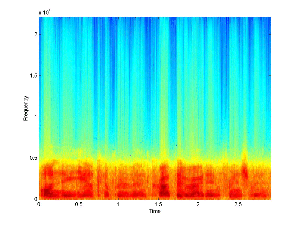
Filtered Message Signal |
Now, recalling techniques from ELEC 241 and what we've
learned this semester, we modulate the filtered message using a
cosine with carrier frequency 20 kHz, the midpoint of our 4 kHz
band. We then combine the modulated, filtered message with the
filtered base signal and we get a signal with a hidden message in
it. The spectrogram of the combined signal is shown below.
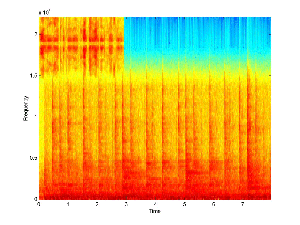
Combined Signal
So, what do we do now? If we are doing digital watermarking,
we are pretty much done. A record label could encode a message
in their songs, making it write-protected and un-recordable. But,
what if we worked for a government agency which wanted to relay a
secret message using our above method? How would you recover the
hidden message?
First, we must get rid of portions of the base signal that
are in the combined signal. We do this by bandpass filtering the
combined signal to above and below the hidden message. Then, we
modulate the message back down, using a cosine with the same
carrier frequency as before. Also, due to additive noise when we
did the addition and higher frequencies due to modulation, we
must lowpass filter the demodulated message. We then have a
signal which very closely resembles the sent message. The
results of this process can be seen in the recovered signal below.
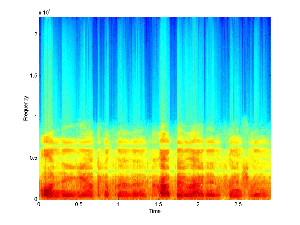
Recovered Signal
This process is a fairly simple one, requiring only
filtering and amplitude modulation in order to hide the signal in
the base. It is very much a physically realizable process and
one that we could accomplish with our current knowledge of
electrical enigeering techniques. This ease of implementation
will more than make up for the small amounts of distortion in the
combined signals, as well as the limited frequency range of the
recovered signal.