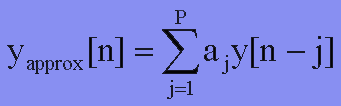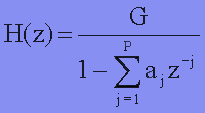Vocal-Tract Characterization by Linear Prediction Coefficients

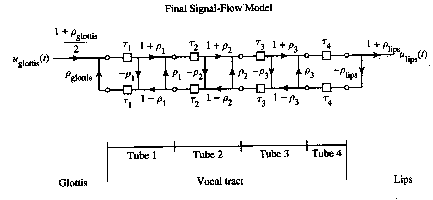
Although the acoustic tube and transmission line model is relatively accurate, its complexity gives us a hard time if we want to do speech synthesis in real-time. We cannot perform calculations on multiple acoustic tubes or cascaded transmission lines very easily. Fortunately, another model exists which greatly simplifies things. Notice that in the transmission line model, a signal flows from source to load via a series of delays. Also, the signal that finally reaches the load (lips) is a linear combination of many reflected and transmitted waves that were created at the transmission line junctions.

This strongly implies that we can model the output of the vocal tract as the summation of past outputs and past and current inputs. If we let Yapprox be the output of the vocal-tract and by simply neglecting the input, we can write the equation:

This is the linear prediction(LP) approximation! The aj's are called the LP coefficients; their weight uniquely characterizes a difference equation.

Now, if we take the z-transform, we can get the transfer function:

This H(z) is the system response of an all-pole filter! If we pass the excitation source through this filter, the source signal will be shaped into our desired utterance. This is the method we use in this project to synthesis speech.

Discrete-Time Model of Synthesis Using Linear Prediction

Figure 4 is a model of speech production using LP analysis.

The excitation signal is either an impulse train or white noise. For voiced speech, the excitation is a periodic impulse train with period equal to the pitch period of speech. This impulse train is passed through a glottal filter that models the air from the lung and vocal folds. After all, the impulses from our vocal folds more closely resembles Fig 5, rather than an impulse train. For unvoiced speech, a white noise signal is produced. There is a switch that leads the desired source to the filter.

Figure 5

The vocal tract filter is characterized the LP coefficients. The radiation filter models the propagation of sound waves once it leaves the lips, but it is neglected in our simplified model. Besides this, the main difference in the filter setup is that we have simplified the pole-zero filter that fully characterizes the vocal tract model into an all-pole filter. The motivation for this is the ease in calculation. Fortunately, this simplification is justified for simple speech synthesis, as the poles are the ones that determine the essential formant peaks in voiced signals. However, by taking out the zeros, we are essentially taking out the nasal cavity, the alternate air passageway, in our simplified model. This filter will be lacking when we wish to synthesize nasal sounds like /m/, and /n/.

In general, since most of the information in a perceived speech results from the vowels, simple speech synthesizer have worked by just concentrating efforts on producing accurate vowels.