Delay Line

IMPORTANT Notice: The Delay Line Model is based on Dr. Julius O. Smith III's paper, Physical Modeling using Digital Waveguides(Reference [1]). Dr. Smith has also kindly offered help in this research. All images on this page are taken from Reference [1], except for the MATLAB plots

 

Introduction

In this project, we physically modeled a string instrument using DELAY LINES. For a detailed explanation of how a delay line works, refer to Dr. Smith's paper. Below is a simple explanation on delay line, and how it applies to our plucked string example.

 

"Physically" plucking a string

When we "physically" pluck a string, the string looks like this:

 image taken from p.3, Reference [1]

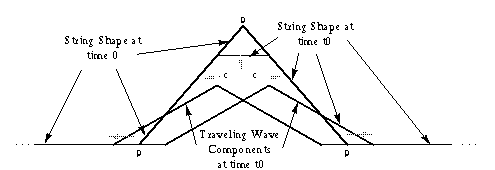
 where we can see that the traveling wave is composed of two components (a left-going wave and a right-going wave). From Physics, we know that the solution to this one-dimensinal traveling wave is

 

y(x,t) = yr(x-ct) + yl(x+ct) (eqn 1)

where yr and yl denote the right and left going waves, respectively.

 

Implementation of Traveling Waves on a String Instrument

To implement this traveling wave model, we need to sample the traveling wave both in the spatial and time domain. (eqn 1) becomes:

 

y[x,t] = yr[n-m] + yl[n+m] (eqn 2)

(note: the brackets [ ] shows that the signals are DISCRETE.)

 This can be implemented by the following model:

 
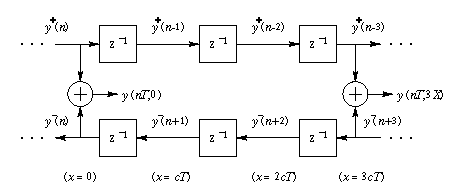
Digital Implementation of an IDEAL, LOSSLESS traveling wave

 On this diagram, the top rail represents the right-going traveling wave in (eqn 2). Each of the z^(-1) corresponds to the delay in (eqn 2). The bottom rail, on the other hand, represents the left-going traveling wave. We can get an output at any discrete instant (spatially and temporally) by summing up the top and bottom rail outputs at that point.

 In the real world, however, there are losses as the wave travels on the string. Therefore, to make the above digital simulation more realistic, we modify it to the following model:

 
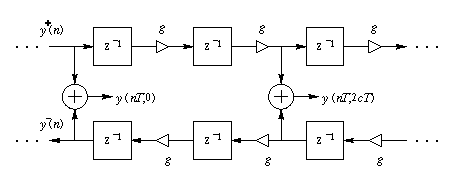
Digital Implementation of an IDEAL, LOSSY traveling wave

 This model is similar to the first model, with one slight modification--we put losses g next to each delay element. Physically, this means that as the wave travels along the string, it experiences losses along the string.

 

Consolidation of Losses/Delay

If we actually implement a plucked string using the above model, we will have very poor results due to rounding errors in EACH delay/loss element. For example, if we are implementing an A (440 Hz) using the above model, we need approximately 100 delay elements PLUS 100 loss elements. (fs/(freq of A) = 44100/440). This can give us very bad result because we need to round off so many numbers. One way to get around this problem is to consolidate the loss/delay elements. The reason we can do this is because each one of these elements are LTI systems, which means we can commute them and get the following:

 
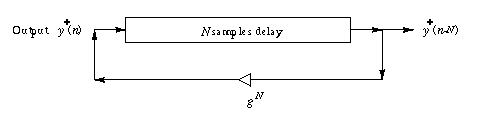
Digital Implementation of a string with consolidated losses and delays

 In this model, we put all the delays together on the top rail and all the losses on the bottom rail. The advantage of doing this is that we will get a better result because we are not rounding off the numbers 100 times like before. Also, this is a lot simpler to implement.

 

What should the LOSSES be?

The N sample delay line is very easy to understand and implement. What model should we use for the losses, g? One thing we know is that not all frequencies damp at the same rate. The higher the frequency, the faster it travels on the string. Hence, the faster it damps and dies out. This fact points to one simple and obvious solution--Lowpass Filters. We will model the losses with a simple one-zero lowpass filter, in the form a + b*z^(-1). We can put a zero at z=-1 to cause the frequency response to reach zero at high frequency (w = pi), as shown in the following z-plane design:

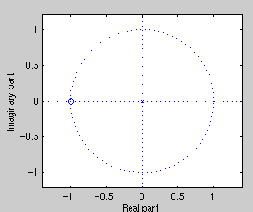 z-plane design of lowpass filter

 If we want to make the frequency response = 1 at w=0, we need:

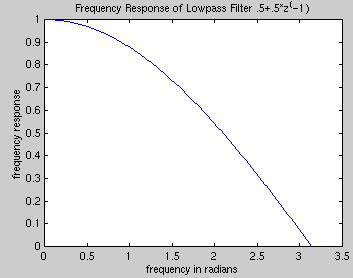 .5 + .5*z^(-1)

Implementing the Model with C Code

We obtain the template of the C Code from Dr. Smith's paper. We edited it to pluck.cc. The first thing that we changed is the format of the output. Instead of sending the output in a Sun/NeXT format, we send our output to a simple array sound file. We have also tried to change different things in the code to find out how that would affect our results. We will mention those changes as we discuss about the result. To use pluck.cc, we give the following inputs: amp(<1.0), pitch(Hz), pickPosition(<1.0), pickupPosition(<1.0), duration(sec), and output_filename.snd. pluck.cc returns a .snd file containing vectors of the note specified by the inputs.

 

Experimentation with pluck.cc and Results

The sampling rate fs that we used is 44100 Hz for CD sound quality. However, at first we had some problems with MATLAB. MATLAB is unable to play a sound vector at the frequency 44100 Hz. We gave an input of 440 Hz (note A) to pluck.cc, with sampling frequency 44100 Hz, but MATLAB was unable to play it back at that rate if we use the sound command. Therefore we changed the sampling frequency in pluck.cc to 8192Hz. Later on, we discovered a MATLAB command resample that can resample at the frequency that we desired. Therefore we eventually changed the sampling frequency in pluck.cc to the frequency we want--44100Hz.

 After generating the note A (440Hz) using pluck.cc and passing the .snd file through MABLAB to generate the graphs and sound, we obtained the following results:

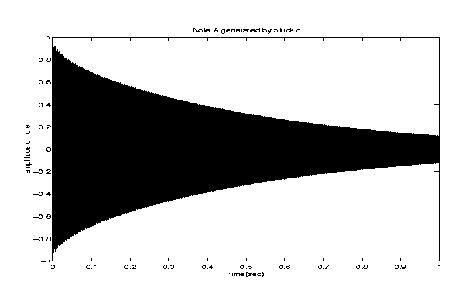 Note A (1 second)

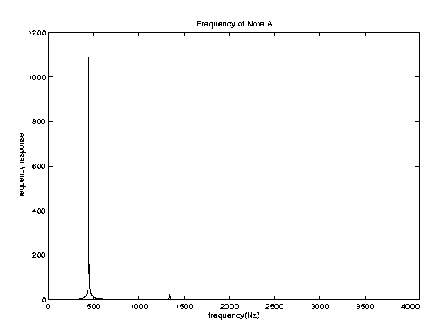 Frequency Response of Note A

 Note that the frequency response peaks at around 440Hz (note A).

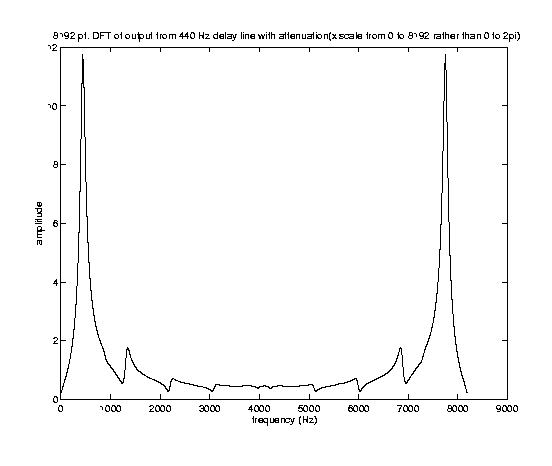
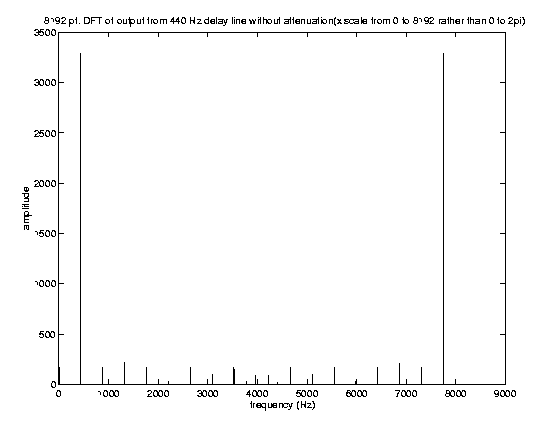
 For experimentation, we tried to design different loss filters. We moved the location of the ZERO of a + b*z^(-1) to different places to implement different lowpass filters. We tried to place the zero at z=-0.1 to decrease attenuation. As expected, note A took a lot longer to die out when z=-0.1. We even rewrite pluck.cc to eliminate ATTENUATION (the lowpass filter). When we did that, the note never died out, as expected. From the frequency spectrum plot below, we can see that when we do not have attenuation, note A is consisted of only certain discrete frequencies. This is in big contrast to the frequency spectrum WITH attenuation, where we see that note A is consisted of all sorts of frequencies.

 
DFT of output from 440Hz Delay Line without Attenuation.

 
DFT of output from 440Hz Delay Line with Attenuation.

 We have discovered something interesting through trying out different sampling rates and zero locations. For a fix desired musical note frequency (for example, note A at 440Hz), we know that w = OMEGA/fs, where OMEGA stands for the analog frequency, w stands for the discrete frequency, and fs stands for the sampling frequency. If we fixed our lowpass loss filter design to .5+.5*z^(-1), by changing the samling rate fs, we got different levels of attenuation. This is because different sampling rates give us different w's. As sampling frequency INCREASES, w DECREASES for a given OMEGA. A lower w corresponds to a lower frequency response magnitude for a fixed lowpass filter design. This lower frequency response magnitude causes the same note (say, 440Hz), to die off a lot faster.

 

Playing Songs

We passed different frequencies through pluck.cc and obtained different sound output files, which we passed to MATLAB to generate the audio sound. Some musical notes were out of tune, especially the ones at high frequencies. To solve this, we need to learn about FRACTIONAL DELAY. Click HERE to find out what we have learned about fractional delay!

 We composed some songs by combining notes together. Mary Had a Little Lamb was a very successful song that we wrote using pluck.cc. This is because the three notes that we used for this song were B(494.7Hz), A(440Hz), and G(392.4Hz), which were at relatively LOW frequencies, and hence tuning was not bad. We also wrote Twinkle Twinkle Little Star but that was not very successful, because we wrote it in G major, which contains the note D at 602.7Hz. This note sounded identical to E (665.3Hz) because of problems that we mentioned in the Fractional Delay section.

 In addition, we were able to combine notes together and play different intervals/chords. Once again, however, notes at high frequencies are not always in tune.

 

This is a Gang Project for Elec431.