Step 4 - Image Comparison Algorithm
In this portion of the algorithm, we take each of our parsed and
standard sized images and identify what number it is. There were two main
steps involved in this process. First, a hole detection algorithm, and
second, the evaluation of lowest variance.
Hole Algorithm
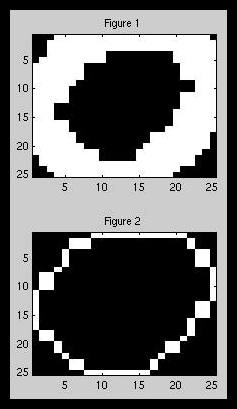 In determining the number of holes, we first use a thinned version of our
standard sized image instead of the normal standard sized. The normal
standard sized has
been thickened to allow for more accurate match comparison, but it tends to
blur the lines, often filling in holes that should be present.
The thinned image takes each line down
to one pixel in thickness allowing all holes to be clearly seen. Figure 1
shows the standard sized, thickened example 0, while Figure 2 has our thinned
version. Unfortunately, the thinning function in Matlab,
bwmorph(img,'thin',Inf), occasionally yielded
problems which are discussed later.
In determining the number of holes, we first use a thinned version of our
standard sized image instead of the normal standard sized. The normal
standard sized has
been thickened to allow for more accurate match comparison, but it tends to
blur the lines, often filling in holes that should be present.
The thinned image takes each line down
to one pixel in thickness allowing all holes to be clearly seen. Figure 1
shows the standard sized, thickened example 0, while Figure 2 has our thinned
version. Unfortunately, the thinning function in Matlab,
bwmorph(img,'thin',Inf), occasionally yielded
problems which are discussed later.
Once we've obtained our thinned image, we use the bweuler(img) command in
matlab to determine the number of holes in the image. This command returns
the Euler (go tennessee) number of the image. This number represents, the number of
objects in the image, minus the number of holes in those objects. Since
all of our objects are one number, completely connected, our number of
objects is one. Thus we can easily derive the number of holes from the
Euler number by subtracting one and taking the absolute value.
 With the number of holes determined we go into a series of if statements to
narrow the field of choices for a given number. For instance, once we've
determined that there are two holes, then we know the number must be an 8.
Similarly, 1 hole indicates, a 0, 2, 4, 6, or 9, and no holes narrows the
choices to 1, 2, 3, 4, 5, 7.
It is generally agreed that the numbers 2 and
4 can either have one or two holes, so they are included in both lists.
For the two and no hole lists, the hole algorithm can not make any further
distinguishments. However, in the one hole case, the location of the hole
can help narrow the field. Since 2 and 6 will only have holes in the bottom
of the image, and 4 and 9 only in the top half, the choices for picking can
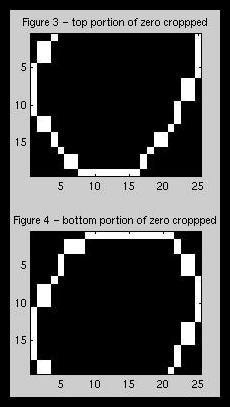
be further narrowed. Our algorithm makes these distinguishments by first
cropping the top portion of the image (figure 3) and determining the number
of holes in the cropped image and then cropping off the bottom portion
of the image and checking the number of holes (figure 4). Once cropped,
the 2s and 6s should still have holes with the top cropped, but not the
bottom. Whereas, 4 an 9 should only still have holes with the bottom
cropped. Zeros will be picked out by the images that lose there hole with
both croppings of the top and the bottom. This subdivision technique has a
few problems as well.
With the number of holes determined we go into a series of if statements to
narrow the field of choices for a given number. For instance, once we've
determined that there are two holes, then we know the number must be an 8.
Similarly, 1 hole indicates, a 0, 2, 4, 6, or 9, and no holes narrows the
choices to 1, 2, 3, 4, 5, 7.
It is generally agreed that the numbers 2 and
4 can either have one or two holes, so they are included in both lists.
For the two and no hole lists, the hole algorithm can not make any further
distinguishments. However, in the one hole case, the location of the hole
can help narrow the field. Since 2 and 6 will only have holes in the bottom
of the image, and 4 and 9 only in the top half, the choices for picking can
be further narrowed. Our algorithm makes these distinguishments by first
cropping the top portion of the image (figure 3) and determining the number
of holes in the cropped image and then cropping off the bottom portion
of the image and checking the number of holes (figure 4). Once cropped,
the 2s and 6s should still have holes with the top cropped, but not the
bottom. Whereas, 4 an 9 should only still have holes with the bottom
cropped. Zeros will be picked out by the images that lose there hole with
both croppings of the top and the bottom. This subdivision technique has a
few problems as well.
Variance Comparison
To make the final decision on what number a particular image represents, we
compare the variances between our unknown image and a set of standard
images. As discussed previously we created a
slew of standard images from averages of various font sets. Once we've
narrowed down the set of possible numbers using the hole algorithm, we use
the computed variances between the unknown and each of the possible numbers
to determine the best guess for the unknown image. We deem the correct
image to be which ever standard image has the lowest variance with the unknown
image. Our computation of variance stems from the traditional
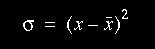
We compute this variance for each of the 25 grid boxes using our standard
sized image and the the standard image created for a given number. This
yields 25 different variances. We merely sum all the variances to get our
total variance between our unknown image and a known standard.
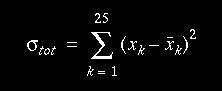
With our total variance computed between our unknown sample and each of the
possible numbers we've narrowed the selection down to (using the hole
algorithm), we take the known number with the minumum variance as our best
guess of what the unknown number is.
Actual Matlab Code -- evalimg3.m
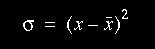
 In determining the number of holes, we first use a thinned version of our
standard sized image instead of the normal standard sized. The normal
standard sized has
been thickened to allow for more accurate match comparison, but it tends to
blur the lines, often filling in holes that should be present.
The thinned image takes each line down
to one pixel in thickness allowing all holes to be clearly seen. Figure 1
shows the standard sized, thickened example 0, while Figure 2 has our thinned
version. Unfortunately, the thinning function in Matlab,
bwmorph(img,'thin',Inf), occasionally yielded
problems which are discussed later.
In determining the number of holes, we first use a thinned version of our
standard sized image instead of the normal standard sized. The normal
standard sized has
been thickened to allow for more accurate match comparison, but it tends to
blur the lines, often filling in holes that should be present.
The thinned image takes each line down
to one pixel in thickness allowing all holes to be clearly seen. Figure 1
shows the standard sized, thickened example 0, while Figure 2 has our thinned
version. Unfortunately, the thinning function in Matlab,
bwmorph(img,'thin',Inf), occasionally yielded
problems which are discussed later.
 With the number of holes determined we go into a series of if statements to
narrow the field of choices for a given number. For instance, once we've
determined that there are two holes, then we know the number must be an 8.
Similarly, 1 hole indicates, a 0, 2, 4, 6, or 9, and no holes narrows the
choices to 1, 2, 3, 4, 5, 7.
It is generally agreed that the numbers 2 and
4 can either have one or two holes, so they are included in both lists.
For the two and no hole lists, the hole algorithm can not make any further
distinguishments. However, in the one hole case, the location of the hole
can help narrow the field. Since 2 and 6 will only have holes in the bottom
of the image, and 4 and 9 only in the top half, the choices for picking can
be further narrowed. Our algorithm makes these distinguishments by first
cropping the top portion of the image (figure 3) and determining the number
of holes in the cropped image and then cropping off the bottom portion
of the image and checking the number of holes (figure 4). Once cropped,
the 2s and 6s should still have holes with the top cropped, but not the
bottom. Whereas, 4 an 9 should only still have holes with the bottom
cropped. Zeros will be picked out by the images that lose there hole with
both croppings of the top and the bottom. This subdivision technique has a
few problems as well.
With the number of holes determined we go into a series of if statements to
narrow the field of choices for a given number. For instance, once we've
determined that there are two holes, then we know the number must be an 8.
Similarly, 1 hole indicates, a 0, 2, 4, 6, or 9, and no holes narrows the
choices to 1, 2, 3, 4, 5, 7.
It is generally agreed that the numbers 2 and
4 can either have one or two holes, so they are included in both lists.
For the two and no hole lists, the hole algorithm can not make any further
distinguishments. However, in the one hole case, the location of the hole
can help narrow the field. Since 2 and 6 will only have holes in the bottom
of the image, and 4 and 9 only in the top half, the choices for picking can
be further narrowed. Our algorithm makes these distinguishments by first
cropping the top portion of the image (figure 3) and determining the number
of holes in the cropped image and then cropping off the bottom portion
of the image and checking the number of holes (figure 4). Once cropped,
the 2s and 6s should still have holes with the top cropped, but not the
bottom. Whereas, 4 an 9 should only still have holes with the bottom
cropped. Zeros will be picked out by the images that lose there hole with
both croppings of the top and the bottom. This subdivision technique has a
few problems as well.
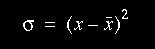
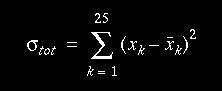


 Previous
Previous