for the linear filtering method were very encouraging but indicate that the method is far from perfect, and the results hinted at how things could be improved. The large number of parameters and passes made determining an absolute quality of the algorithm impossible. However, the effects of each of the parameters could be quite easily observed, and allow for effective adjustment by hand.
The alteration that made the algorithm the easiest to work with was finding out how to normalize the entire filter to allow the adjustment parameters to alter things independently. For example, initially the comb filters were not normalized to have an identical mean value, and thus depending on the frequency and width of the pulses, the mean would move. This meant for different signals the scaling coefficient on the threshold curves had to be readjusted.
The first pass of the algorithm is usually quite accurate. The ECG signals are relatively clean, so simply picking out the large pulses relative to the noise floor will pick the majority out. Using this data, the pulses can be characterized enough to decide how much of the power is noise and how much is the pulses. The threshold curve from the simple one pulse comb can be shifted to fit just above this and dip down into the top of the pulse, thus rejecting more noise, or it can cut deeper being less resilient to noise. This method also ensures that if the heart is beating with a smaller ECG in an area the threshold doesn't get stuck at such a high level no beats are detected, and if the noise gets too great, the threshold isn't driven up too much.
The recursive passes don't just look at amplitude characteristics, but also look at how much a certain region is running at a given frequency. This allows the algorithm to lock in and get a stronger match when it is running at the right frequency.
The amount the algorithm follows various parameters is easily controlled. For example, the mean of the combs determines how much the threshold curves will cut down in response to a spike above the noise floor. However, setting the mean too low will make the threshold move down too much over a small spike, and will artificially cut out a pulse from the 0 line. Setting it too high will not allow the algorithm to change the threshold when it thinks there is a pulse, so will make it equally susceptible to a region of high noise as a single spike. There is another coefficient that is scaled against the threshold in all cases. This can be approximated to sensitivity, and usually is left near 1. Changing the number of filter banks has a large effect on the computation time, but also can allow more accurate frequency resolving and locking on in weaker SNR conditions. By adjusting how much the center point is emphasized in the comb filters, the amount that algorithm converges based on point amplitude, as opposed to the amplitudes of surrounding peaks can be adjusted.
Overall, the method worked very well. In some test files, at around 300 beats per minute over 300 seconds only one error would be made. It would generally catch a frequency even in a fair amount of noise, depending on the settings.
The match filter sometimes worked very well and improved results immensely, especially for small time windows. However, it seems like generally the nature of a heart pulse is too variable, so as the sequence went on the pulse would change shape and become increasingly filtered out.
The algorithm was tested on short samples from both dog and human as well, and as long as the physiological bounds were correctly specified, worked just as well.
Graphs
The first set of graphs are on a cleaner signal

After the first pass on clean data. It locks onto all of the ECG beats.
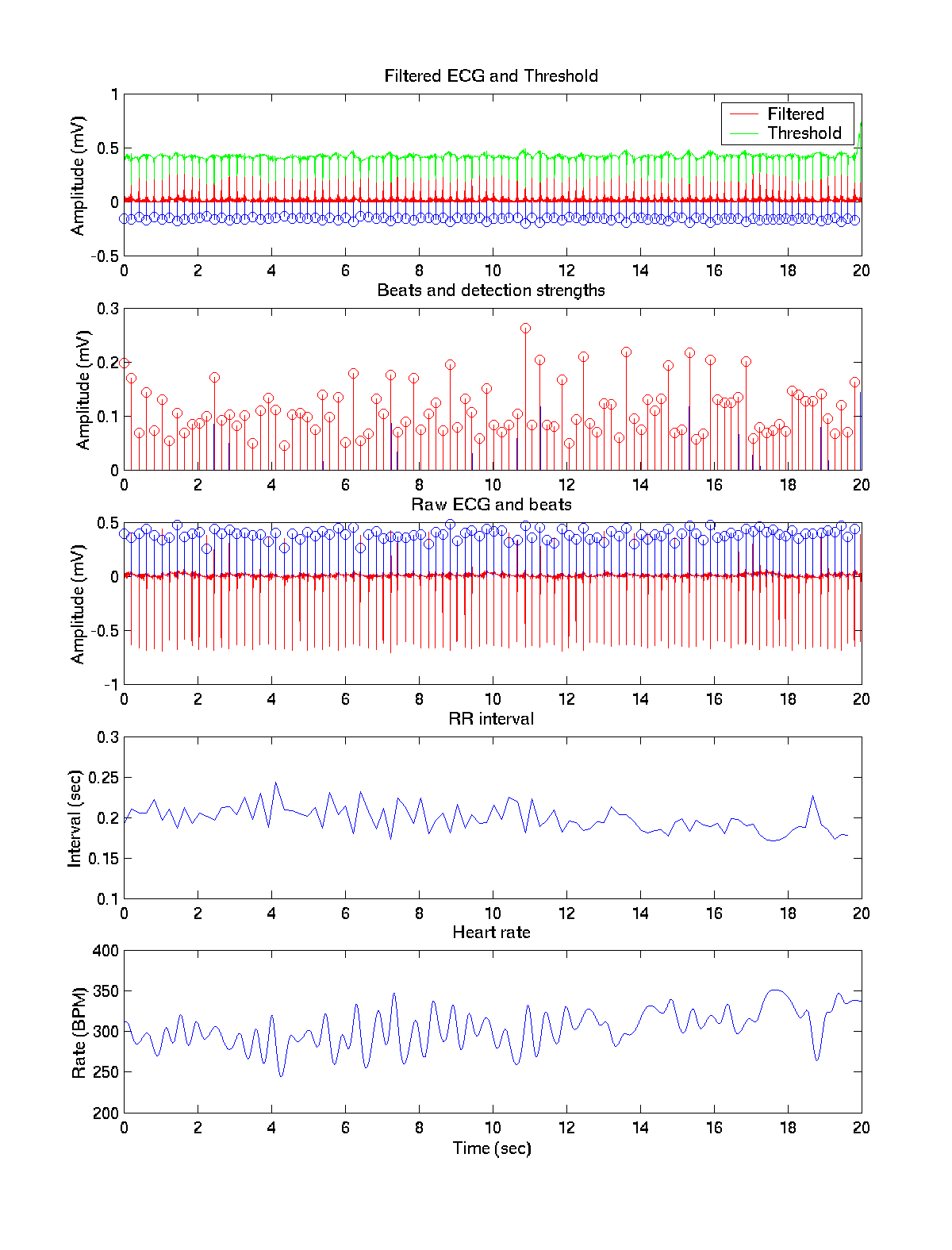
After the second pass on clean data. You can see the threshold shift up and become normalized although it still dips down enough at each pulse that they go above threshold. This prevents detecting beats in the noise that just result in a large average, or from shifting the floor up too far and not detecting anything.
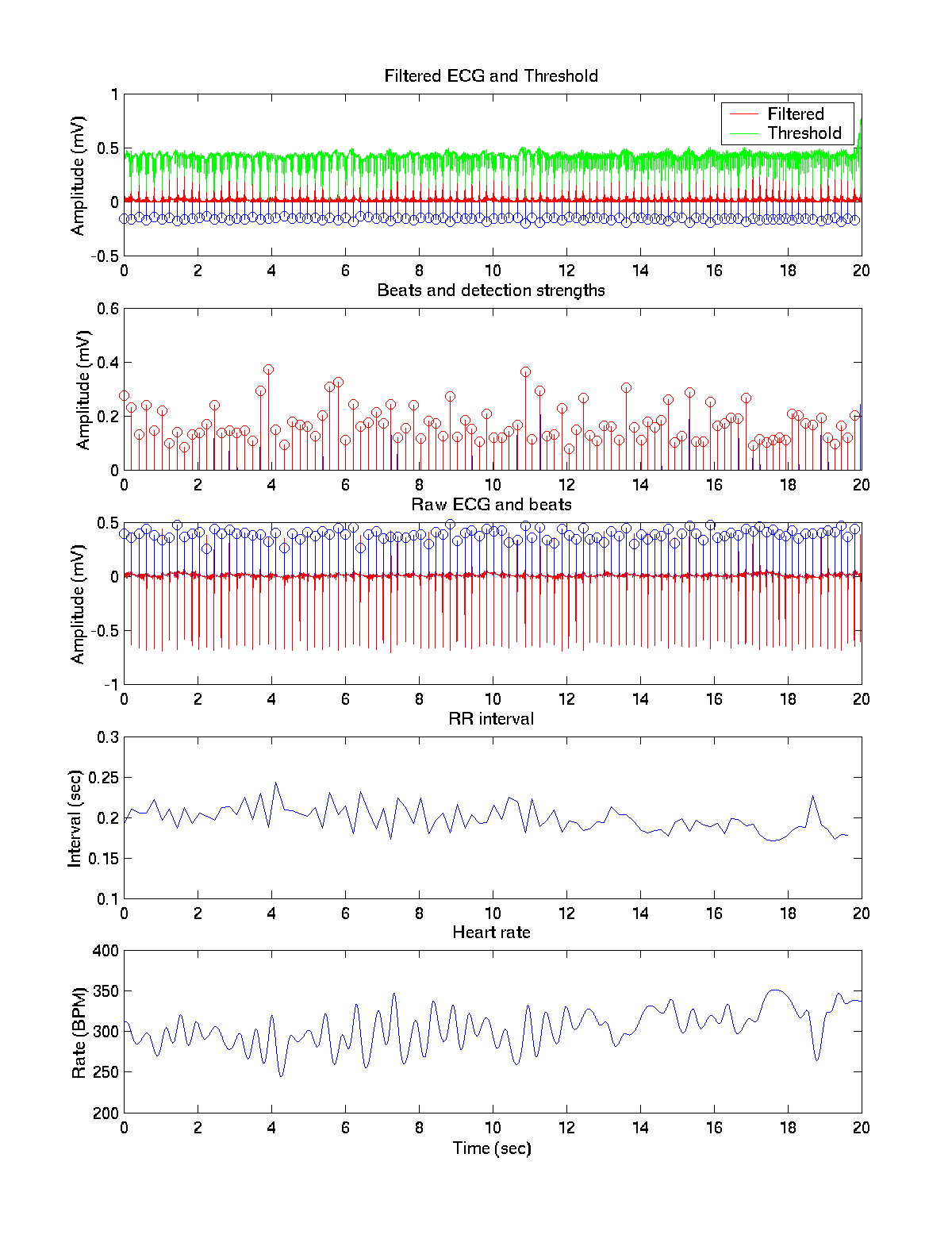
After filtering with the comb filters. Notice that there seems to be more noise on the threshold curve, but it stays overall higher than without the comb filter.
The second set of graphs are on a noisier signal
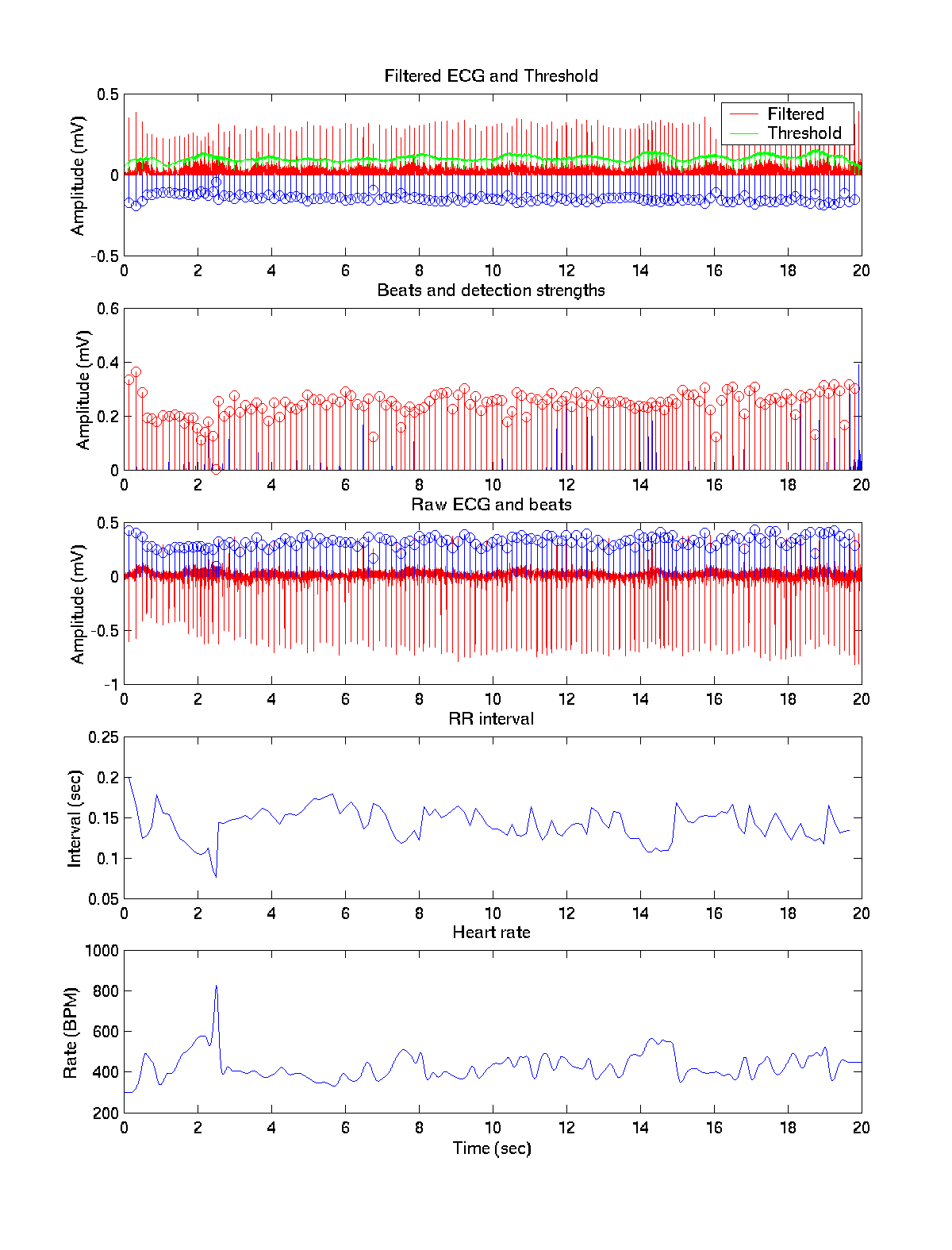
The sharp discontinuities up to 1000 indicate that the algorithm picks up some of the noise in the signal as a heart beat. Normalizing against the noise floor should remove this.
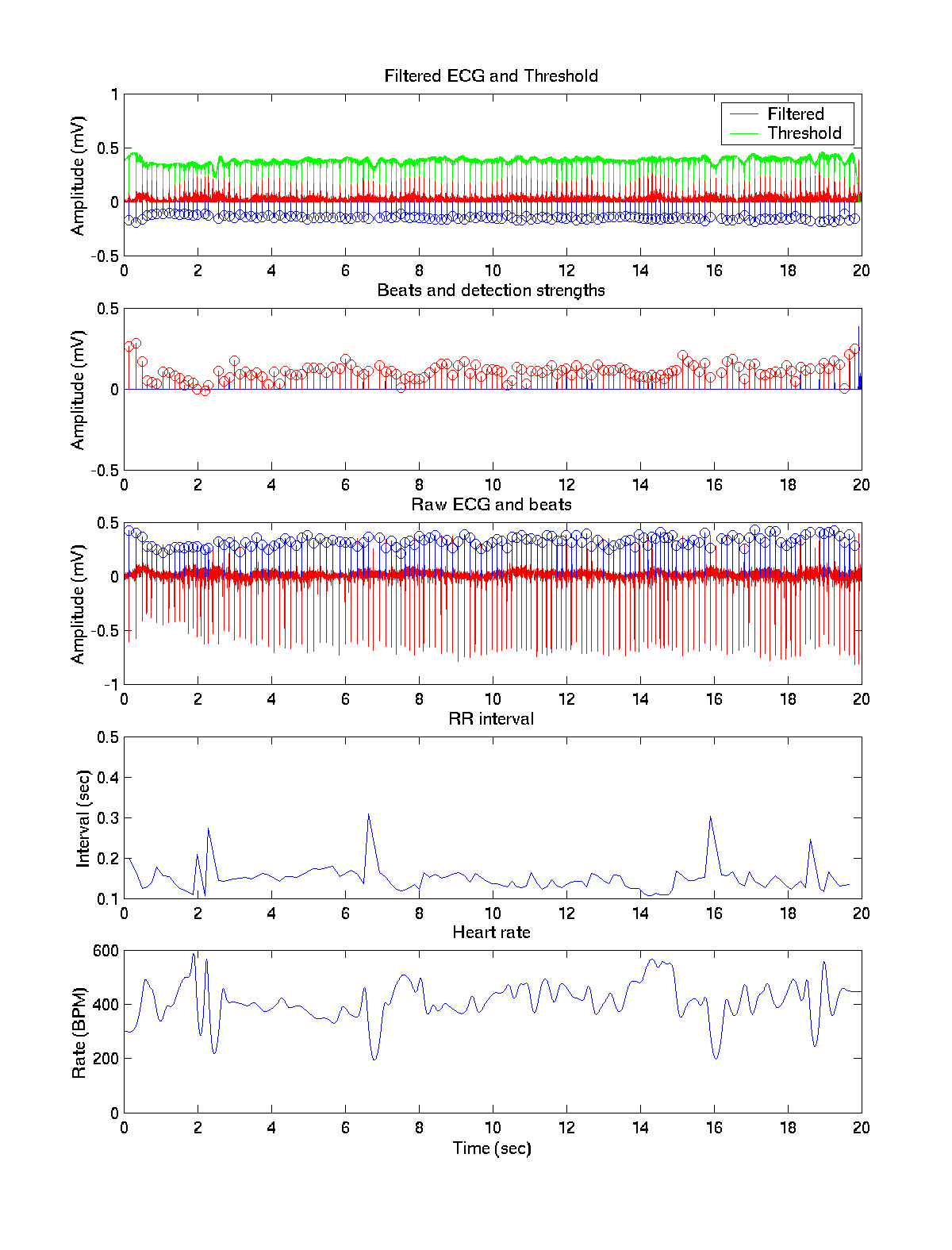
As predicted the false beats are not detected anymore. However, some real beats are not detected. In the next step, the algorithm will use what it knows about the frequency to try and lock on.
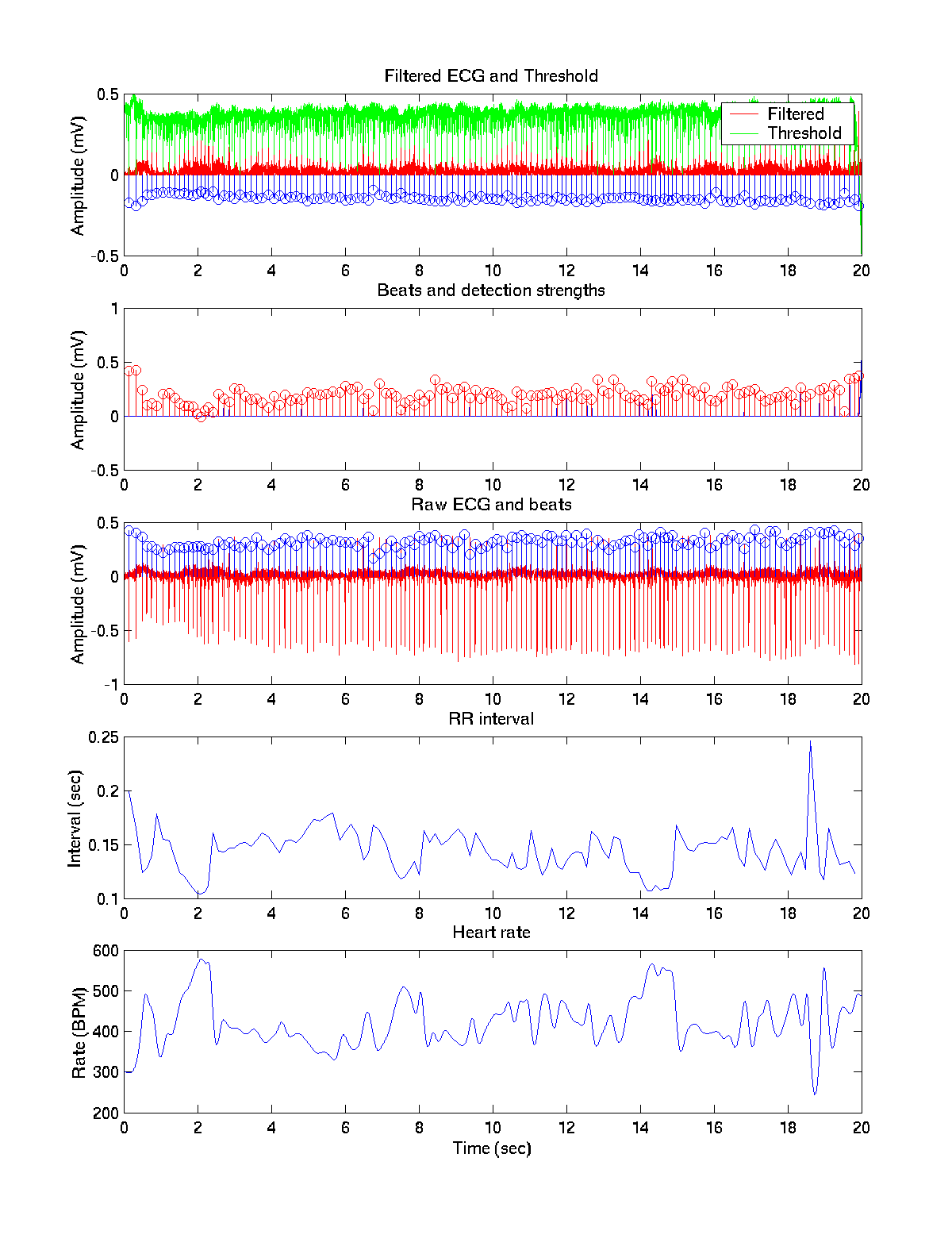
As desired, the final pass detects the correct beats from the noise, but not those that have almost as much amplitude out of beat.