Navigation:
Introduction/Overview
Process
Application
Synthetic vs. Natural
Comparison
Conclusions
MATLAB Code
Extras
Comparison
Part of the importance of the EMD is the way it decomposes signals over which Fourier Transforms stumble. Because of the way the EMD keeps signals in their own domain, it can deal with signals which would otherwise be considered "poorly-behaved." When a signal enters a new domain, the way certain select characteristics change with the original variable are totally lost. While the signal may be accurately retrieved, the signal cannot be effectively analyzed in the new domain without this information.
The EMD does not have this problem. When it decomposes a time-domain signal into IMFs, for instance, each mode function contains information about how the frequency of the original signal changes in time. Because of this, the EMD needs not assume the slightest pretention towards linearity or time-invariance.
Here we provide an example to illustrate this property. Below is a chunk of the Fourier Transform of the data from the vector ecg.mat:
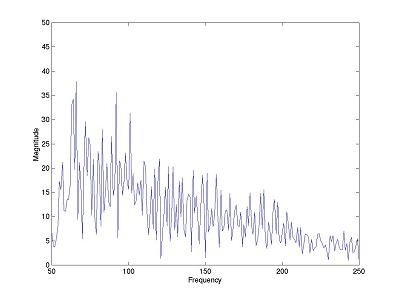
Even when we know what we should find in this domain, that being spikes (or at least some hint of local maxima) at the fundamental heartbeat, we cannot find it. We see only noise. This is because the fundamental beat changes its frequency enough with time that such a spike does not show up. Clearly the EMD is superior in this case.