
Group :
Commando

Group Members:
Nadathur Varadarajan - npraja@rice.edu
Sanjay Sahasrabudhe - sanjay@ruf.rice.edu
- info
Walter A. Caro - wcaro@alumni.rice.edu
- info
Project II Time-Frequency
Analysis
Short Time Fourier Transform :
Mathematically the short time fourier transform is defined as:
![]()
where ,
x is the signal;
w is the window function.
The STFT is the most convenient time frequency representation to use of the five we tested, since it takes comparatively less time and gives high resolution output.
1. The first signal example we used to test our STFT implementation was the chirp signal provided. The STFT tracks the frequency content of the signal extremely well.
2. The second example was the third story displacement
of a scaled down three story building subject to a chirp signal (0.5 Hz
to 6.5 Hz.). The natural frequency of the structure is 5 Hz in the first
mode. Thus when the frequency of the ground motion matches the frequency
of the structure i.e 5 Hz. resonance occurs. And the STFT clearly identifies
the resonance.
Discrete Wavelet Transform :
The DWT is based on local sums and local differences given by :
![]()
where,
xo and x1 are adjacent samples. The procedure that we followed to implement the DWT was to shift a copy of the signal by 1 sample and subtract it from the original signal. The results, the sums and differences, were down-sampled by a factor of two in order to correct for the redundant values that this procedure generates. The first and last samples were taken out in order to obtain correct vector lengths. Also, in order to get the correct results, one condition is that the length of the signal vector needs to be a power of 2. Therefore we zero padded the input signals inside our function. As you can see in our plots we included both the vector and matrix representations of the DWT. The matrix representation is generated by setting up a matrix of height equal to the number of levels in the wavelet coefficient decomposition and width equal to length of the last differences vector. A short algorithm performs mapping between the vector form of the DWT and itís matrix form.
As a side note we should mention that we could also have implemented the DWT using a couple of length 2 FIR filters.
1. In the chirp signal from the matrix representation of the DWT we can see that there are components with increasing frequency in the 15 Hz to 30 Hz. range.
2. In the displacement signal the existence of 2 resonant conditions is very easy to locate in the time domain but hard to correctly identify in the frequency axis. We can see however that the frequency of the two spicks in the signal is the same.
The advantage of the DWT over the STFT is the smaller time it requires
to be computed. But the disadvantage is the poor frequency resolution.
Continuous Wavelet Transform :
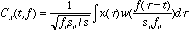
where the Morlet wavelet is defined as :
![]() .
.
To compute the CWT, the convolution of the input signal and the wavelet specified needs to be computed for different values of frequency. A fast way to compute the convolution is to take the Inverse Fast Fourier Transform of the product of the Fast Fourier Transforms of the signal and the wavelet. Since the convolution performs the time shift for us, we donít need to give the time shift as an input the wavelet function. Not obvious from the equation is that the scaling factor s is easily computed from the frequency and the center frequency of the wavelet. The use of the Fast Fourier Transform makes the CWT fast and easy to compute.
A problem that we encountered is that the center frequency of the wavelet affects the frequency axis display in the CWT making it hard to know what the actual frequencies are in the signal; in contrast the STFT determines the frequencies by itself. The CWT however is good for observing transients.
1. The CWT of the chirp signal shows approximately the same behavior as the STFT except for the vertical bands resulting from the use of wavelets. Each sharp edge in the signal shows a spike in the CWT matrix.
2. The CWT of the displacement signal shows the correct locations in
the time axis for the frequency components. However because of the center
frequency of the wavelet is little lower from the actual frequencies shown
in the SFFT Since there are no transients the CWT does not work upto itís
potential in the displacement signal but it is in the chirp signal.
Wigner Distribution :
The Wigner Distribution was reinvented by Ville in 1948 and it is also called as Wigner - Ville distribution.
Mathematically the wigner distribution is given as :
![]()
Here, the signal itself is taken as a window i.e. ![]() .
.
1. From the wigner distribution of the chirp signal it can be seen that the effect of the cross components is negligible and the wigner distribution tracks the frequency content of the signal very well. Excellent. That's because this signal is really good and simple.
2. In the displacement signal also the wigner distribution is effective
in frequency tracking since the main component of the signal is 5 Hz. Here
also the effect of cross components is negligible. The signal is also very
good and nice, so the pictures are very nice too.