• Definition
• Uses

• Frequency Domain
• Time Domain

• Frequency Conclusions
• Time Conclusions

• Work Distribution
• C.J. Ganier
• Randall Holman
• Julie Rosser
• Erik Swanson

          For CD quality sound, it is necessary to encode 16 bits per 
     sample at a rate of 44.1kHz.  However, sound can also be recorded
     at 8 bits per sample.  Since the majority of the sound signal is 
     stored in the M most significant bits of the sound code,
     changing the lowest N significant bits, where N can be any power
     of two up to M/2 bits, leaves the sound signal somewhat changed in
     quality and definition, but still recognizeable, and often
     indistinguishable from the original.  

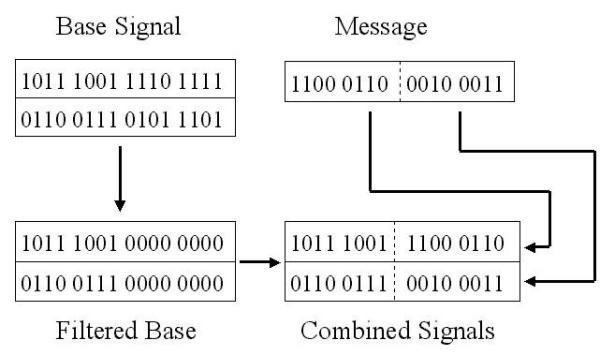
          Starting once again with two signals, a Base signal and a
     Messages signal, we choose a value for N, the number of least
     significant bits that we wish to replace in the encoding, and
     choose an appropriate length base.  The reason for choosing an
     appropriate length base is to make sure that the full message can
     be encoded.  The length of the base must be B, the total number of
     encoded bits in the message, divided by N, the number of bits to be
     replaced in the Base, multiplied by the length of the Message.
     This is merely a minimum requirement.  The Base is allowed to be
     longer.  

          Below you will find the Base and Message Signals for our
     time domain example.

          Starting out, we take the Matlab vectors which are decimal
     values between 1 and -1 and add 1 to every single one of them.
     After adding 1 to each number to make them all greater than zero
     we multiply by 2^(B-1) and convert each one to a binary number.  
     Taking the binary number mod (1-N), N still being the bits to be 
     replaced, we zero out the N least significant bits.  
          After the N least significant bits of the base are zeroed
     out, we chunk each message signal in binary into B/N separate
     chunks. We then add the now B/N times longer Message signal to
     the Base signal thus returning a combined signal.  This combined
     signal is then translated back into Matlab vectors by doing the 
     first steps in reverse.  

          Now that we have the message signal hidden inside of the
     Base signal we need to come up with a way to get Message
     signal back.  Assuming perfect transmission (see results),
     the recovery of our message signal is quite simple.    

          Start by adding 1 to each Matlab vector convert decimal to
     binary by multiplying by 2^(B-1) and converting to binary.  Then
     we go through every signal and concatenate the N least
     significant bits of every Received Base signal into binary
     message signals of length B.  Covert these binary numbers back to
     decimal and shift back down to 1 to -1 and we now have a
     perfectly recovered message! 

          This process is a relatively simple one to conceive, but
     harder than the frequency domain process to implement in
     real life.  (Without DSP).  Granted that we have perfect
     transmission we have a recovered signal that is as perfect
     as the orginally sent message.