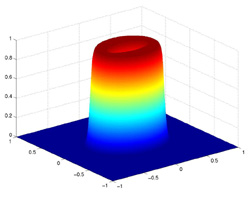
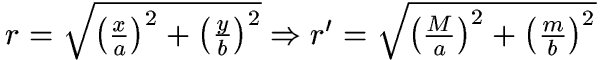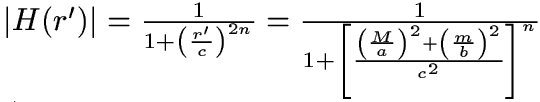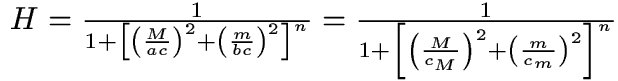Designing filters in 2D simply involves taking basic filter design
techniques and basing them around the two dimensional frequency, which
is the Cartesian distance from the origin, equal to the square root of
the sum of the squares.
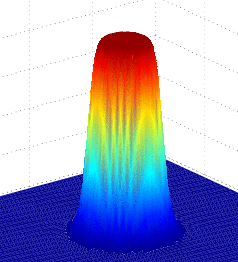
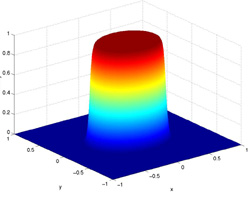
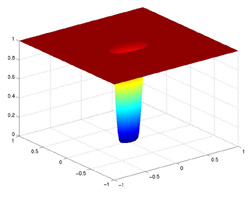
In a circularly oriented filter, i.e. one which is equally potent in all
directions, the cutoff frequency remains a fixed number. However,
when designing elliptically oriented filters, i.e. filters which have varying
effectiveness at different angles, the cutoff frequency becomes a
function of the angle.
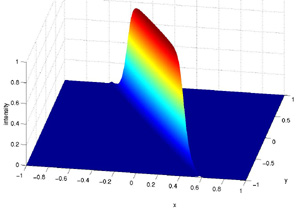
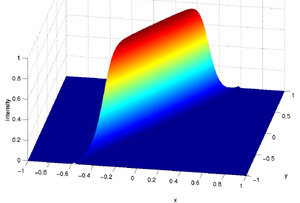
One of the easiest class of filters to work with in two dimensions
are Butterworth filters. Beginning with the equation for an ellipse,
we now rotate our coordinate axes from (x,y) to (M,m) where M is the
direction of the major axis and m the direction of the minor axis.
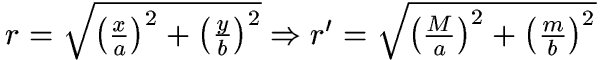
From here, we substitute the elliptical radius at this point into
the equation for the magnitude of a Butterworth filter. Notice that
we are designing these filters as magnitude only, no phase, due to the
fact that phase spreading will strongly degrade the image.
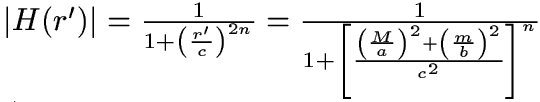
And now we continue to combine terms and substitute in two cutoff
frequencies instead of one: one for the major axis, and one for the
minor.
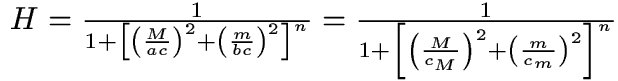
This gives us our completed formula for design of a lowpass
Butterworth filter of elliptical shape in 2D. By using an elliptical
filter instead of the circular ones we used in previous examples, we
can create strongly directional filters.