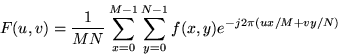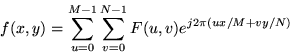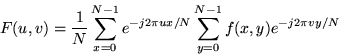Instead of talking about one dimensional signals that represent changes in amplitude in time, here we are dealing with two dimensional signals which represent intensity variations in space. These signals come in the form of images. The images we will deal with here are digital, and thus have a finite width and hieght in pixels, which we will assume have a real number value. Because our signals are discrete, we will need an analog of the one dimensional DFT for two dimensional signals. This analog is the following pair of transforms:

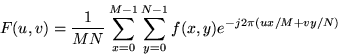
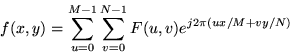
Thus an MxN image has an MxN set of (complex) fourier coefficients. To implement this transform, we would like an analog of the FFT, which will let us quickly compute the coefficients of the transform. In fact, we can do better. The two dimensional DFT is seperable into two one dimensional DFTs which can be implemented with an FFT algorithm.
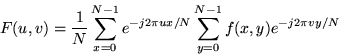