As with the one dimensional DFT, there are many properties of the transformation that give insight into the content of the frequency domain representation of a signal and allow us to manipulate singals in one domain or the other.

Shift Property See an example As in one dimension, there is a simple relationship that can be derived for shifting an image in one domain or the other. Since both the space and frequency domains are considered periodic for the purposes of the transforms, shifting means rotating around the boundaries. The equations describing this are:

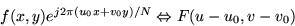
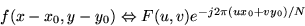
Scale Property See an example Just as in one dimension, shrinking in one domain causes expansion in the other for the 2D DFT. This means that as an object grows in an image, the corresponding features in the frequency domain will expand. The equation governing this is:

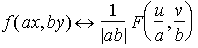
Rotation Property See an example This is a property of the 2D DFT that has no analog in one dimension. Becuase of the seperability of the transform equations, the content in the frequency domain is positioned based on the spatial location of the content in the space domain. This means that rotating the spatial domain contents rotates the frequency domain contents. This can be formally described by the following relationship:
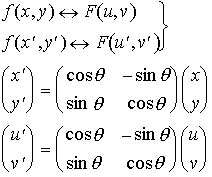