Loris for Your Cough
Background
McAulay-Quatieri Method
Bandwidth Enhancement
Algorithm
Loris Application
Our Algorithm
Results
Conclusion
Poster
Group
Reassigned
Bandwidth-Enhanced Method
The Reassigned Bandwidth-Enhanced Method, developed by Kelly Fitz of Washington State University, resolves the noise modeling problems associated to the MQ method[1] .
Using the MQ method, signals are represented by a collection of sinusoidal components, which is called partial. The peaks in the spectrum of each window are linked together (Short Time analysis). If the signal being represented has obvious high peaks or a trend in the frequencies from window to window this analysis provides an accurate reconstruction. However, if a signal has significant energy outside the peaks, or very high frequency noise, the MQ method does not represent the signal adequately. These signals are said to be noisy. The energy that is not capable of being represented is called noisy energy since it has frequencies with fast-varying amplitude. These types of signals require many sinusoids to be represented sufficiently. The sinusoids that do represent them become a track of short duration partials with rapidly varying amplitudes and frequencies. It is difficult to distinguish the noisy tracks due to external unwanted noise from the short jittery tracks that are due to the wanted sound representation. The sinusoidal model does not provide a way of distinguishing noisy components from deterministic components. In addition, the representation of these noisy signals is very fragile. Time and frequency manipulation changes phase, which destroys the properties of the sound and introduces errors in the reconstructed signal.
To provide a better way of representing noise, the Reassigned Bandwidth-Enhanced Method uses Bandwidth Enhanced Oscillators, which spread spectral energy away from the partialís center frequency (Figure 1). The partialís energy is increased while the bandwidth also increases relative to its spectral amplitude. The center frequency stays the same so that frequency is spread evenly on both sides. By removing the noisy tracks and increasing the bandwidth of neighboring tracks, the energy in the signal is conserved and a closer representation to the original signal can be constructed.
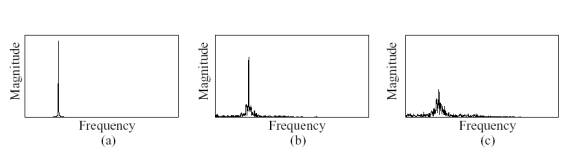
Figure
1
These Bandwidth Enhanced Oscillators can now be used to synthesize a sound signal from components that have varying frequencies, amplitudes and concentrations of noise and sinusoidal energy. A greater variety of sounds can now be represented with greater accuracy while still using the sinusoidal model for the representation or longer, more well defined tracks. These Bandwidth-Enhanced partials allow us to manipulate noise representations without taking away the desired noise representations. The Enhanced-Bandwidth Sinusoidal Model allows for appropriate representation of noise that provides a way to distinguish the non-sinusoidal noise that must be removed.