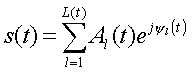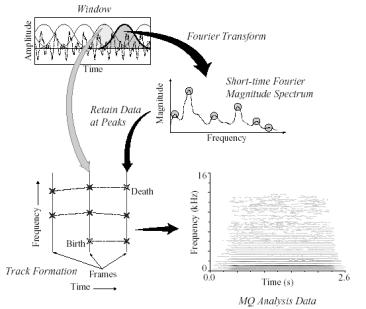
McAulay-Quatieri Method

Typical sort time Fourier analysis involves windowing pieces of a continuous time signal and computing its Continuous Time Fourier Transforms to get a local in time frequency composition.  Windows must be chosen that minimizes the amount of included frequency content from outside the window in time (side-lobe interference). Manipulating the information involves standard methods (low-pass filters, etc).  Synthesis is accomplished by computing Inverse Fourier Transforms of each section and special additive techniques are utilized to recombine the altered windows.

In 1986 Robert McAulay and Thomas Quatieri proposed a new method of analysis/synthesis for continuous time speech signals which attempted to develop a reconstruction process that would result in an “as close as possible” approximation of the original signal[1].  They modeled speech signals as two components.  The first was an excitation signal which consisted of a sum of sinusoids with time-varying amplitudes and frequencies, as well as an initial phase offset. The second component is the voice track which is modeled as a time-variant filter with time-varying magnitudes and phase.  These two components are combined and expressed as:

Equation 1

Where A_l(t) combines the time-varying magnitude response of the vocal track and the amplitude of the excitation signal, and the phase of the exponential includes the time-varying phase of the vocal track as well as the initial phase offset of the excitation signal.

To find expressions for these sinusoids they derived a new technique to analyze the signal.  Using overlapping windowing methods similar to standard short time analysis, the MQ method computes Fourier transforms of the individual windows.  The peak frequencies of each window (the partials) are found and their amplitudes and phases are extracted.  The partials for each window are linked to those in the following window in order to develop a trend in the progression of frequencies (their amplitude and phases).  We call each progression a track.  The birth of a track occurs when there does not exist a partial in the previous window with which to connect one in the current window.  Conversely, a death track occurs when a partial does not exist in the following window with which to connect one in the current window (Figure 1).

Figure 1[2]

To generate the sign waves each point is connected smoothly by interpolating between them using a cubic function.  This gives us continuous functions that describe the progression of the amplitude, phase, and frequency of our signal.  We use these to construct a sign wave and then weighted by a triangle window with a width of twice that of the window.

The MQ Model has outstanding results and reproduces inaudibly different signals when applied to a wide variety of quasi-harmonic sounds.  Perhaps its greatest advantage is the small amount of data required to perform this process.  To reproduce a signal using standard Fourier techniques information about a great many coefficients must be retained.  To reconstruct perfectly an infinite number must be used.  With the MQ method information about several time varying sinusoids must be stored, and little else.

One of the flaws in the MQ method is how it represents noise.  Noise shows up as tracks that span only a small number of windows.  It is difficult to represent these short tracks using sinusoids so other methods must be developed (see section entitled Bandwidth-Enhancement).