Loris Under the Hood

Loris is a software application used to alter sound.  Its technology is based off of the ideas discussed in the reassigned enhanced bandwidth method.  A graphical user interface, FOSSA, was created so that users can get a graphical feel for the manner in which Loris alters sound files.  Before the code of Loris is explained, some of the classes in Loris's hierarchy need to be described in relation to the methods that we use.

BreakPoint Class

• The breakpoint class represents a partial's value at a specific time.  The breakpoint holds the time-invariant amplitude, frequency, and phase of the partial at a specific time.

Partial Class

• The partial class is the track of a partial (as described earlier) with time.  It primarily consists of an iteration of BreakPoints (described earlier).  This iteration is the progression of the partial with time.  The partial is merely a linear interpolation along these breakpoints.  The partial class has methods to find its amplitude, frequency, and phase at a specific time.  (It linearly interpolates between breakpoints to find these values.)  The partial class also has methods to add Breakpoints to its iterator.  For more information look at the API after the code has been downloaded.

PartialList Class

• The partial list class is a list of partial objects.  The user can specifically access any partial in the list desired, and there is also functionality to add Partials to the list.

Loris representation of Sound

 Loris takes in a sound file in either .aiff or .sdif format.  It represents the files as a collection of breakpoints (with no connectivity yet.)

As of yet no analysis has been done on the sound.  Next Loris uses a Channelizer class which creates a set of overlapping windows "for signal analysis".  The Channelizer matches peak frequencies in subsequent windows and gives respective matched frequencies the same label.  After the channelizer has made its pass on the sound file, Loris then uses a Distiller to map breakpoints with matching labels into iterators of breakpoints and placed in different partials.  Then these partials are clumped together in a list representing the entire sound file.  Loris dilates "short lived" signals, i.e. noise, into longer partials - interpolating values in windows where the respective partial does not resides.

For our goals in this project this last feature was undesired.  So we created an algorithm in Python that runs after the above processes and returns a list of Partials that we want.  Here's the code.

 

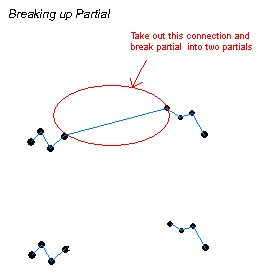
First our algorithm goes and breaks up the partials into smaller segments if need be.  If a there is a large gap between breakpoints then the partial is split between the two breakpoints.

After the Partials have been broken up into smaller partials, noise is now represented as "short lived" partials.  So our algorithm makes a pass through the list of partials and puts the partials that have a lifetime longer than a given threshold and adds them to an "inCrowd" list of partials; otherwise, it adds the partial to the "outCrowd" list of partials.  After this pass, the algorithm then proceeds to check to see if any of the partials in the "outCrowd" are close of enough to any members of the "inCrowd" or their harmonics.  This approach allows us to keep harmonics of a tone in melodious music (which is desirable.)  Keeping the harmonics of a tone keeps the "richness" of the sound.

The "closeness" of two partials is determined locally with respect to the time period in which both partials are alive (if there is no overlap then it assumed that the partials are not close at all).  The average frequency of both partials in the given time period is then calculated and if the distance between these average values is less than a defined threshold then the partial in the "outCrowd" is now added to the "inCrowd".  After this pass is done we have a list of partials that should have less noise in it.